This page provides detailed descriptions of various measures of magnitude and related (specifically diameter) outputs of the SDSS photometry pipelines.
- The SDSS asinh magnitude system (aka luptitude)
- The PSF Magnitude (psfMag)
- The Fiber Magnitude (fiberMag )
- The Petrosian Magnitude (petroMag )
- The Model Magnitude (deVMag, expMag,modelMag,CModelMag)
- Which Magnitude should I use?
The SDSS asinh magnitude system
All magnitudes within the SDSS are expressed as inverse hyperbolic sine (or “asinh”) magnitudes, described in detail by Lupton, Gunn, & Szalay (1999) and in the SDSS DR6 algorithms page. They are sometimes referred to informally as luptitudes. The transformation from linear flux density measurements to asinh magnitudes is designed to be virtually identical to the standard astronomical magnitude at high signal-to-noise ratio, but to behave reasonably at low signal-to-noise ratio and even at negative values of flux density, where the logarithm in the Pogson magnitude fails. This allows SDSS to report a flux density even in the absence of a formal detection; they quote no upper limits in their photometry.
The asinh magnitudes are characterized by a softening parameter b, the typical 1-sigma noise of the sky in a PSF aperture in 1" seeing. The relation between flux density f and asinh magnitude m is
Here, f0 is the zero point of the magnitude scale, i.e., f0 is the flux density of an object with magnitude of zero, given in the table below. The quantity b is measured relative to f0, and thus is dimensionless.
The corresponding flux density uncertainty iswhere dm is the uncertainty in SDSS magnitude m.
IMPORTANT: The DR5 and DR6 magnitudes, fluxes, and flux uncertainties were updated in the 2012 September NED release, to correct three issues:
- The u band CModel magnitudes and z band PSF and Model magnitudes were restored to original SDSS values, removing zero-point corrections mzpc of -0.04 to the u band CModel magnitudes and +0.02 to the z band PSF and Model magnitudes. These corrections are instead applied to the flux densities, via the f0 values in the table below. This has the effect of restoring the original zero-flux density magnitudes, but also means that the u and z band magnitudes are not strictly on the AB system.
- The correct softening parameters b are now applied, which has the effect of shifting the u, g, i, and z zero-flux magnitudes back to their correct values.
- The flux density uncertainties are now calculated using the formula above, from the derivative of the formula for flux density. This gives more accurate uncertainties near zero flux density, and ensures that these uncertainties are positive.
| Band | b | f0(Jy) | mzpc | Zero-Flux-Density Magnitude [m(f/f0 = 0)] | m(f/f0 = 10b) |
| u | 1.4 × 10-10 | 3767. | -0.04 (CModel magnitudes only) | 24.63 | 22.12 |
| g | 0.9 × 10-10 | 3631. | 0.00 | 25.11 | 22.60 |
| r | 1.2 × 10-10 | 3631. | 0.00 | 24.80 | 22.29 |
| i | 1.8 × 10-10 | 3631. | 0.00 | 24.36 | 21.85 |
| z | 7.4 × 10-10 | 3565. | 0.02 (PSF and Model magnitudes only) | 22.83 | 20.32 |
Fiber magnitudes
The flux contained within the aperture of a spectroscopic fiber (3" in diameter) is calculated in each band.
Notes
- For children of deblended galaxies, some of the pixels within a 1.5" radius may belong to other children; the flux of the parent is measured at the position of the child; this properly reflects the amount of light which the spectrograph will see.
- Images are convolved to 2" seeing before fiberMags are measured. This also makes the fiber magnitudes closer to what is seen by the spectrograph.
Model magnitudes
The computation of model magnitudes in the DR1 and EDR processing had a serious bug which implied that model magnitudes from the EDR and DR1 should not be used for scientific analysis. For DR2 and later, all the imaging data (including EDR and DR1) have been processed through a new version of the SDSS imaging pipeline, that most importantly fixes an error in the model fits to each object. The result is that the model magnitude is now a good proxy for point spread function (PSF) magnitude for point sources, and Petrosian magnitude (which have larger errors than model magnitude) for extended sources.
Just as the PSF magnitudes are optimal measures of the fluxes of stars, the optimal measure of the flux of a galaxy would use a matched galaxy model. With this in mind, the code fits two models to the two-dimensional image of each object in each band:
- A pure deVaucouleurs profile
I(r) = I0 exp{-7.67 [(r/re)1/4]}
(truncated beyond 7re to smoothly go to zero at 8re, and with some softening within r=re/50). - A pure exponential profile
I(r) = I0 exp(-1.68r/re)
(truncated beyond 3re to smoothly go to zero at 4re.
Each model has an arbitrary axis ratio and position angle. Although for large objects it is possible and even desirable to fit more complicated models (e.g., bulge plus disk), the computational expense to compute them is not justified for the majority of the detected objects. The models are convolved with a double-Gaussian fit to the PSF, which is provided by psp. Residuals between the double-Gaussian and the full KL PSF model are added on for just the central PSF component of the image. These fitting procedures yield the quantities
- r_deV and r_exp, the effective (half-light) radii of the models;
- ab_deV and ab_exp, the axis ratio of the best fit models;
- phi_deV and phi_exp, the position angles of the ellipticity (in degrees East of North).
- deV_L and exp_L, the likelihoods associated with each model from the chi-squared fit;
- deVMag and expMag, the total magnitudes associated with each fit.
Note that these quantities correctly model the effects of the PSF. Errors for each of the last two quantities (which are based only on photon statistics) are also reported. The SDSS algorithms apply aperture corrections to make these model magnitudes equal the PSF magnitudes in the case of an unresolved object.
CModel magnitudes
The code now also takes the best fit exponential and de Vaucouleurs fits in each band and asks for the linear combination of the two that best fits the image. The coefficient (clipped between zero and one) of the de Vaucouleurs term is stored in the quantity fracDeV in the CAS. (In the flat files of the DAS, this parameter is misleadingly termed fracPSF.) This allows SDSS to define a composite flux:
where FdeV and Fexp are the de Vaucouleurs and exponential fluxes (not magnitudes) of the object in question. The magnitude derived from Fcomposite is referred to below as the CModel magnitude (as distinct from the model magnitude, which is based on the better-fitting of the exponential and de Vaucouleurs models in the r band).
In order to measure unbiased colors of galaxies, the algorithms measure their flux through equivalent apertures in all bands. The algorithms choose the model (exponential or deVaucouleurs) of higher likelihood in the r filter, and apply that model (i.e., allowing only the amplitude to vary) in the other bands after convolving with the appropriate PSF in each band. The resulting magnitudes are termed modelMag. The resulting estimate of galaxy color will be unbiased in the absence of color gradients. Systematic differences from Petrosian colors are in fact often seen due to color gradients, in which case the concept of a global galaxy color is somewhat ambiguous. For faint galaxies, the model colors have appreciably higher signal-to-noise ratio than do the Petrosian colors.
There is now excellent agreement between CModel and Petrosian magnitudes of galaxies, and CModel and PSF magnitudes of stars. CModel and Petrosian magnitudes are not expected to be identical, of course; as Strauss et al. (2002) describe, the Petrosian aperture excludes the outer parts of galaxy profiles, especially for elliptical galaxies. As a consequence, there is an offset of 0.05-0.1 mag between CModel and Petrosian magnitudes of bright galaxies, depending on the photometric bandpass and the type of galaxy. The rms scatter between model and Petrosian magnitudes at the bright end is now between 0.05 and 0.08 magnitudes, depending on bandpass; the scatter between CModel and Petrosian magnitudes for galaxies is smaller, 0.03 to 0.05 magnitudes. For comparison, the code that was used in the EDR and DR1 had scatters of 0.1 mag and greater, with much more significant offsets.
The CModel and PSF magnitudes of stars are in good agreement (they are forced to be identical in the mean by aperture corrections, as was true in older versions of the pipeline). The rms scatter between model and PSF magnitudes for stars is much reduced, going from 0.03 mag to 0.02 magnitudes, the exact values depending on bandpass. In the EDR and DR1, star-galaxy separation was based on the difference between model and PSF magnitudes. The algorithms now do star-galaxy separation using the difference between CModel and PSF magnitudes, with the threshold at the same value (0.145 magnitudes).
Due to the way in which model fits are carried out, there is some weak discretization of model parameters, especially r_exp and r_deV. This is yet to be fixed. Two other issues (negative axis ratios, and bad model magnitudes for bright objects) have been fixed since the EDR.
Petrosian magnitudes
This is stored as petroMag. For galaxy photometry, measuring flux is more difficult than for stars, because galaxies do not all have the same radial surface brightness profile, and have no sharp edges. In order to avoid biases, it is necessary to measure a constant fraction of the total light, independent of the position and distance of the object. To satisfy these requirements, the SDSS has adopted a modified form of the Petrosian (1976) system, measuring galaxy fluxes within a circular aperture whose radius is defined by the shape of the azimuthally averaged light profile.
The SDSS defines the “Petrosian ratio” RP at a
radius r from the center of an object to be the ratio of the
local surface brightness in an annulus at r to the mean
surface brightness within r, as described by Blanton et al. 2001a, Yasuda et al. 2001:
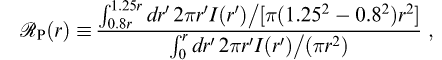
where I(r) is the azimuthally averaged surface brightness profile.
The Petrosian radius rP is defined as
the radius at which RP(rP) equals some
specified value RP,lim, set to 0.2 in this
case. The Petrosian flux in any band is then defined as the flux
within a certain number NP (equal to 2.0 in
this case) of r Petrosian radii:
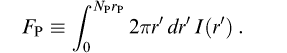
In the SDSS five-band photometry, the aperture in all bands is set by the profile of the galaxy in the r band alone. This procedure ensures that the color measured by comparing the Petrosian flux FP in different bands is measured through a consistent aperture.
The aperture 2rP is large enough to contain nearly all of the flux for typical galaxy profiles, but small enough that the sky noise in FP is small. Thus, even substantial errors in rP cause only small errors in the Petrosian flux (typical statistical errors near the spectroscopic flux limit of r ~17.7 are < 5%), although these errors are correlated.
The Petrosian radius in each band is the parameter petroRad, and the Petrosian magnitude in each band (calculated, remember, using only petroRad for the r band) is the parameter petroMag.
In practice, there are a number of complications associated with this definition, because noise, substructure, and the finite size of objects can cause objects to have no Petrosian radius, or more than one. Those with more than one are flagged as MANYPETRO; the largest one is used. Those with none have NOPETRO set. Most commonly, these objects are faint (r > 20.5 or so); the Petrosian ratio becomes unmeasurable before dropping to the limiting value of 0.2; these have PETROFAINT set and have their “Petrosian radii” set to the default value of the larger of 3" or the outermost measured point in the radial profile. (All of these flags associated with the SDSS photometry are displayed on NED's photometry pages for each SDSS object.)
Finally, a galaxy with a bright stellar nucleus, such as a Seyfert galaxy, can have a Petrosian radius set by the nucleus alone; in this case, the Petrosian flux misses most of the extended light of the object. This happens quite rarely, but one dramatic example in the EDR data is the Seyfert galaxy NGC 7603 = Arp 092, at RA(2000) = 23:18:56.6, Dec(2000) = +00:14:38.
How well does the Petrosian magnitude perform as a reliable and complete measure of galaxy flux? Theoretically, the Petrosian magnitudes defined here should recover essentially all of the flux of an exponential galaxy profile and about 80% of the flux for a de Vaucouleurs profile. As shown by Blanton et al. (2001a), this fraction is fairly constant with axis ratio, while as galaxies become smaller (due to worse seeing or greater distance) the fraction of light recovered becomes closer to that fraction measured for a typical PSF, about 95% in the case of the SDSS. This implies that the fraction of flux measured for exponential profiles decreases while the fraction of flux measured for deVaucouleurs profiles increases as a function of distance. However, for galaxies in the spectroscopic sample (r<17.7), these effects are small; the Petrosian radius measured by frames is extraordinarily constant in physical size as a function of redshift.
PSF magnitudes
These are stored as psfMag. For isolated stars, which are well-described by the point spread function (PSF), the optimal measure of the total flux is determined by fitting a PSF model to the object. In practice, SDSS does this by sync-shifting the image of a star so that it is exactly centered on a pixel, and then fitting a Gaussian model of the PSF to it. This fit is carried out on the local PSF KL model at each position as well; the difference between the two is then a local aperture correction, which gives a corrected PSF magnitude. Finally, SDSS uses bright stars to determine a further aperture correction to a radius of 7.4" as a function of seeing, and applies this to each frame based on its seeing. This involved procedure is necessary to take into account the full variation of the PSF across the field, including the low signal-to-noise ratio wings. Empirically, this reduces the seeing-dependence of the photometry to below 0.02 mag for seeing as poor as 2". The resulting magnitude is stored in the quantity psfMag. The flag PSF_FLUX_INTERP warns that the PSF photometry might be suspect. The flag BAD_COUNTS_ERROR warns that because of interpolated pixels, the error may be under-estimated.
Which Magnitude should I use?
NED has chosen to display the PSF, Model, CModel, and Petrosian magnitudes for the SDSS objects that have them (not all objects have all of these magnitudes given in the SDSS data tables). Here is more information from the SDSS documentation concerning the choice of magnitude and the associated diameters.
Faced with this array of different magnitude measurements to choose from, which one is appropriate in which circumstances? There are no guarantees regarding what is appropriate for the science you want to do, but here are some examples, using the general guideline that one usually wants to maximize some combination of signal-to-noise ratio, fraction of the total flux included, and freedom from systematic variations with observing conditions and distance.
Given the excellent agreement between CModel magnitudes (see CModel magnitudes above) and PSF magnitudes for point sources, and between CModel magnitudes and Petrosian magnitudes (albeit with intrinsic offsets due to aperture corrections) for galaxies, the CModel magnitude is now an adequate proxy to use as a universal magnitude for all types of objects. As it is approximately a matched aperture to a galaxy, it has the great advantage over Petrosian magnitudes, in particular, of having close to optimal noise properties.
Example magnitude usage
- Photometry of Bright Stars: If the objects are bright enough, add up all the flux from the profile profMean and generate a large aperture magnitude. It is recommended to use the first 7 annuli.
- Photometry of Distant Quasars: These will be unresolved, and therefore have images consistent with the PSF. For this reason, psfMag is unbiased and optimal.
- Colors of Stars: Again, these objects are unresolved, and psfMag is the optimal measure of their brightness.
- Photometry of Nearby Galaxies: Galaxies bright enough to be included in the spectroscopic sample have relatively high signal-to-noise ratio measurements of their Petrosian magnitudes. Since these magnitudes are model-independent and yield a large fraction of the total flux, roughly constant with redshift, petroMag is the measurement of choice for such objects. In fact, the noise properties of Petrosian magnitudes remain good to r=20 or so.
- Photometry of Galaxies: Under most conditions, the CModel magnitude is now a reliable estimate of the galaxy flux. In addition, this magnitude account for the effects of local seeing and thus are less dependent on local seeing variations.
- Colors of Galaxies: For measuring colors of extended objects, it is recommended that you use the model (not the CModel) magnitudes; the colors of galaxies were almost completely unaffected by the DR1 software error. The model magnitude is calculated using the best-fit parameters in the r band, and applies it to all other bands; the light is therefore measured consistently through the same aperture in all bands.
Of course, it would not be appropriate to study the evolution of galaxies and their colors by using Petrosian magnitudes for bright galaxies, and model magnitudes for faint galaxies.