3.5. Perturbations

The technology for calculating the production of inhomogeneities during inflation is by now very well understood (For an excellent review see [11]). The natural variables to follow are the Fourier transformed density contrasts (k) in comoving coordinates (k_co = a k_phys). A given mode (k) behaves very differently depending on its relationship to the Hubble radius R_H 1/H. During inflation H = const. while comoving scales are growing exponentially. The modes of interest start inside R_H (k >> R_H^-1) and evolve outside R_H (k < R_H^-1) during inflation. After inflation, during the SBB, R_H t and a t^1/2 or t^2/3 so R_H catches up with comoving scales and modes are said to ``fall inside'' the Hubble radius.

It is important to note that R_H is often called the ``horizon''. This is because in the SBB R<sub>H</sub> is roughly equal to the distance light has traveled since the big bang. Inflation changes all that, but ``Hubble radius'' and ``horizon'' are still often (confusingly) used interchangeably.

Modes that are relevant to observed structures in the Universe started out on extremely small scales before inflation. By comparison with what we see in nature today, the only excitations one expects in these modes are zero-point fluctuations in the quantum fields. Even if they start out in an excited state, one might expect that on length-scales much smaller (or energies-scales much higher) than the scale (^1/4) set by the energy density the modes would rapidly ``equilibrate'' to the ground state. These zero-point fluctuations are expanded to cosmic scales during inflation, and form the ``initial conditions'' that are used to calculate the perturbations today. Because the perturbations on cosmologically relevant scales must have been very small over most of the history of the Universe, linear perturbation theory in GR may be used. Thus the question of perturbations from inflation can be treated by a tractable calculation using well-defined initial conditions.

One can get a feeling for some key features by examining this result which holds for most inflationary models:

(9)

Here _H² is roughly the mean squared value of when the mode falls below R_H during the SBB. The ``*'' means evaluate the quantity when the mode in question goes outside R<sub>H</sub> during inflation, and V is the inflaton potential. Since typically the inflaton is barely moving during inflation, <sub>H</sub><sup>2</sup> is nearly the same for all modes, resulting in a spectrum of perturbations that is called ``nearly scale invariant''. The cosmological data require _H 10^-5.

In typical models the ``slow roll'' condition,

(10)

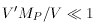
is obeyed, and inflation ends when V'M_P / V 1. If V is dominated by a single power of during the relevant period V'M_P / V 1 means M_P at the end of inflation. Since typically does not vary much during inflation M_P would apply throughout. With these values of , and assuming simple power law forms for V, one might guess that the right side of Eqn. 9 is around unity (as opposed to 10^-5!) Clearly some subtlety is involved in constructing a successful model.

I have noticed people sometimes make rough dimensional arguments by inserting V M_G⁴ and V' M_G³ into Eqn. 9 and conclude _H (M_G / M_P)³. This argument suggests that _H is naturally small for GUT inflation, and that the adjustments required to get _H 10^-5 could be modest. However that argument neglects the fact that the slow roll condition must be met. When this constraint is factored in, the challenge of achieving the right amplitude is much greater than the simplest dimensional argument would indicate.