

Prior to the discovery of the expansion of the Universe there was little that cosmology could contribute to the question of extraterrestrial life aside from probabilities and prejudices. After our discovery of the expansion and evolution of the Universe the situation changed significantly. The entire cosmic environment was recognised as undergoing steady change. The history of the Universe took on the complexion of an unfolding drama in many acts, with the formations of first atoms and molecules, then galaxies and stars, and most recently, planets and life. The most important and simplest feature of the overall change in the Universe that the expansion produces is the rate at which it occurs. This is linked to the age of the expanding universe and that of its constituents.
In the 1930s, the distinguished biologist JBS Haldane took an interest in
Milne's proposal
[1]
that there might exist two different
timescales governing the rates of change of physical processes in the
Universe: one, t, for ``atomic'' changes and another,  , for
``gravitational changes'' where
, for
``gravitational changes'' where  =
ln (t / t0) with t0 constant.
Haldane explored how changing from one timescale to the other could alter
ones picture of when conditions in the Universe would become suitable for
the evolution of biochemical life
[2],
[4].
In particular, he
argued that it would be possible for radioactive decays to occur with a
decay rate that was constant on the t timescale but which grew in
proportion to t when evaluated on the
=
ln (t / t0) with t0 constant.
Haldane explored how changing from one timescale to the other could alter
ones picture of when conditions in the Universe would become suitable for
the evolution of biochemical life
[2],
[4].
In particular, he
argued that it would be possible for radioactive decays to occur with a
decay rate that was constant on the t timescale but which grew in
proportion to t when evaluated on the  scale. The biochemical
processes associated with energy derived from the breakdown of adenosine
triphosphoric acid would yield energies which, while constant on the t
scale, would grow as t2 on the
scale. The biochemical
processes associated with energy derived from the breakdown of adenosine
triphosphoric acid would yield energies which, while constant on the t
scale, would grow as t2 on the  scale. Thus there would be an
epoch of cosmic history on the
scale. Thus there would be an
epoch of cosmic history on the  scale before which life was
impossible but after which it would become increasingly likely. Milne's
theory subsequently fell into abeyance although the interest in gravitation
theories with a varying Newtonian ``constant'' of gravitation led to detailed
scrutiny of the paleontological and biological consequences of such
hypothetical changes for the past history of the Earth
[4].
Ultimately, this led to the formulation of the collection of ideas now known
as the Anthropic Principles,
[5],
[6].
scale before which life was
impossible but after which it would become increasingly likely. Milne's
theory subsequently fell into abeyance although the interest in gravitation
theories with a varying Newtonian ``constant'' of gravitation led to detailed
scrutiny of the paleontological and biological consequences of such
hypothetical changes for the past history of the Earth
[4].
Ultimately, this led to the formulation of the collection of ideas now known
as the Anthropic Principles,
[5],
[6].
Another interface between the problem of the origin of life and cosmology has been the perennial problem of dealing with finite probabilities in situations where an infinite number of potential trials seem to be available. For example, in a universe that is infinite in spatial volume (as would be expected for the case for an expanding open universe with non-compact topology), any event that has a finite probability of occurring should occur not just once but infinitely often with probability one if the spatial structure of the Universe is exhaustively random [3]. In particular, in an infinite universe we conclude that there should exist an infinite number of sites where life has progressed to our stage of development. In the case of the steady-state universe, it is possible to apply this type of argument to the history of the universe as well as its geography because the universe is assumed to be infinitely old. Every past-directed world line should encounter a living civilisation. Accordingly, it has been argued that the steady state universe makes the awkward prediction that the universe should now be teeming with life along every line of sight [4].
The key ingredient that modern cosmology introduces into considerations of
biology is that of time. The observable universe is expanding and
not in a steady state. The density and temperature are steadily falling as
the expansion proceeds. This means that the average ambient conditions in
the universe are linked to its age. Roughly, in all expanding universes,
dimensional analysis tells us that the density of matter,  , is
related to the age t measured in comoving proper time and Newton's
gravitation constant, G, by means of a relation of the form
, is
related to the age t measured in comoving proper time and Newton's
gravitation constant, G, by means of a relation of the form
The expanding universe creates an interval of cosmic history during which
biochemical observers, like ourselves, can expect to be examining the
Universe. Chemical complexity requires basic atomic building blocks which
are heavier than the elements of hydrogen and helium which emerge from the
hot early stages of the universe. Heavier elements, like carbon, nitrogen,
and oxygen, are made in the stars, as a result of nuclear reactions that
take billions of years to complete. Then, they are dispersed through space
by supernovae after which they find their way into grains, planets, and
ultimately, into people. This process takes billions of years to complete
and allows the expansion to produce a universe that is billions of light
years in size. Thus we see why it is inevitable that the universe is seen to
be so large. A universe that is billions of years old and hence billions of
light years in size is a necessary pre-requisite for observers based upon
chemical complexity. Biochemists believe that chemical life of this sort,
and the form based upon carbon in particular, is likely to be the only sort
able to evolve spontaneously. Other forms of living complexity (for example
that being sought by means of silicon physics) almost certainly can exist
but it is being developed with carbon-based life-forms as a catalyst rather
than by spontaneous evolution.
The inevitability of universes that are big and old as habitats for life
also leads us to conclude that they must be rather cold on average because
significant expansion to large size reduces the average temperature
inversely in proportion to the size of the universe. They must also be
sparse, with a low average density of matter and large distances between
different stars and galaxies. This low temperature and density also ensures
that the sky is dark at night (the so called ``Olbers' Paradox'' first noted
by Halley, [7])
because there is too little energy available in
space to provide significant apparent luminosity from all the stars. We
conclude that many aspects of our Universe which, superficially, appear
hostile to the evolution of life are necessary prerequisites for the
existence of any form of biological complexity in the Universe.
Life needs to evolve on a timescale that is intermediate between the typical
time scale that it takes for stars to reach a state a state of stable
hydrogen burning, the so called main-sequence lifetime, and the timescale on
which stars exhaust their nuclear fuel and gravitationally collapse. This
timescale, t*, is determined by a combination of
fundamental constants of Nature
where mN is the proton mass, h is Planck's
constant, and c is the velocity of light
[8],
[4]
In expanding universes of the Big Bang type the reciprocal of the observed
expansion rate of the universe, Hubble's constant H0
The fact that the age t0 

 70 km s-1 Mpc-1, is closely related to the
expansion age of the
universe, t0, by a relation of the form
70 km s-1 Mpc-1, is closely related to the
expansion age of the
universe, t0, by a relation of the form
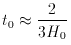
 1010 yr
deduced from observations of
H0 in this way is a little larger than the main
sequence lifetime, t*, is entirely natural in the Big
Bang theory that is, we observe a little
later than the time when the Sun forms). However, the now defunct steady
state theory, in which there is no relation between the age of the universe
(which is infinite) and the measured value of H0,
would have had to
regard the closeness in value of H0-1 and
t* as a complete coincidence
[9].
1010 yr
deduced from observations of
H0 in this way is a little larger than the main
sequence lifetime, t*, is entirely natural in the Big
Bang theory that is, we observe a little
later than the time when the Sun forms). However, the now defunct steady
state theory, in which there is no relation between the age of the universe
(which is infinite) and the measured value of H0,
would have had to
regard the closeness in value of H0-1 and
t* as a complete coincidence
[9].