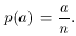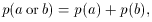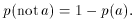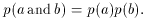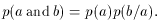Classical or a priori probabilities are defined in terms of the possible outcomes of a trial, recognized in advance as equally probable. In the toss of a coin, the probability of getting a head is 1/2: the number of outcomes that give a head, 1, divided, by the total number of possible outcomes, head or tail, 2. In the toss of a die, the probability of getting one dot is 1/6: the number of outcomes that give one dot, 1, divided by the total number of possible outcomes, one through six dots, 6. In general, the probability of event a is
where a is the number of equally probable outcomes that
satisfy criteria a, and n is the total number of equally
probable outcomes.
In the examples just given, the outcomes are mutually
exclusive; i.e., only one outcome is possible at a time. If
events a and b are mutually exclusive, then
and
For the toss of a coin, p(head or tail) = p(head)
+ p(tail) = 1, and p(not head) = 1 - p(head) = 1/2. For
the toss of a die, p(1 dot or 2 dots) = p(1 dot)
+ p(2 dots) = 1/3, and p(not 1 dot) = 1 - p(1 dot)
= 5/6.
In these examples, the outcomes also are statistically
independent; i.e., the occurrence of one event does not
affect that of another. If events a and b are statistically
independent, then
The probability of obtaining heads in each of two tosses
of a coin is (1/2)(1/2) = 1/4. The probability of obtaining
a single dot in each of two tosses of a die is
(1/6)(1/6) = 1/36.
Events are conditional if the probability of one event
depends on the occurrence of another. If the probability
that b will occur, given that a has occurred, is
p(b/a), then the probability that both will occur is
For example, the probability of drawing two aces from
a deck of cards is (4/52)(3/51) = 1/221. If the first card
were put back into the deck and the deck reshuffled, then
the probability of drawing the second ace would not be
conditioned on the drawing of the first, and the
probability would be (4/52)(4/52) = 1/169, in accord with Eq. A.4.
Here are some rules of thumb for dealing with
compound events, when the events are both mutually
exclusive and statistically independent: