Annu. Rev. Astron. Astrophys. 1992. 30: 51-74 Copyright © 1992 by Annual Reviews. All rights reserved

3. WAVES AND MODES IN DISKS

The best way to obtain insight into the self-consistent excitations of a disk is to replace the disk by a collection of spinning, concentric rings with the same overall surface density and angular momentum distribution. ⁽¹⁾ Each ring i is characterized by two coordinates, the polar angles _i and _i associated with its normal. For any set of values of these angles and their time derivatives it is straightforward to determine the system's gravitational potential energy V({_i, _i}) and it's kinetic energy K({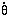_i, _i}), and thus to determine the Lagrangian and equations of motion.

Now there are two ways forward. Either one finds the system's normal modes by linearizing the equations of motion and assuming that all coordinates vary harmonically (Sparke 1984a). Or one can integrate the equations of motion from arbitrarily chosen initial conditions.