Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
51-74 Copyright © 1992 by Annual Reviews. All rights reserved |
3.2 Continuum Modes and the Initial-Value Problem
In the limit as the number of rings in the representation of a disk tends
to infinity, there will always be long-wavelength modes whose frequencies
cluster together to form a continuum. What is the physical significance of
these modes? It is natural to expect their wavefunctions
z (x, y) to
be smooth functions of frequency. Now when one disturbs a disk in any way,
for example by having a companion galaxy pass close by, the amount of energy
fed into each mode is proportional to the square of the overlap integral
(x, y) to
be smooth functions of frequency. Now when one disturbs a disk in any way,
for example by having a companion galaxy pass close by, the amount of energy
fed into each mode is proportional to the square of the overlap integral
between the mode's wavefunction and the forcing term f(x). If
z
Actually the situation is rather more complex and interesting than this
naive analysis suggests. When all is said and done, we are not so much
interested in normal modes per se as in their relation to the
initial-value problem; galaxies are only tens to hundreds of dynamical times
old, so there is no requirement for warps to be immortal, it is sufficient
for them to be reasonably enduring. A set of normal modes can be used to
solve the general initial-value problem only if it is complete.
Van Kampen's (1955)
resolution of the problem posed by the normal modes of an electrostic
plasma shows that the complete set of modes of a collisionless system
involves objects that do not satisfy a dispersion relation, and have
distinctly peculiar wavefunctions.
Vlasov's (1945)
search for a plasma's normal modes led him to an undefined
integral, which he rather arbitrarily interpreted as a Cauchy principal value.
Landau (1946)
argued that Vlasov should have deflected his
integration contour around the integrand's singularity in such a way as to
obtain damped modes.
Van Kampen (1955)
pointed out that Landau's solutions
could not be normal modes, since the system is stable and time-reversible,
which implies that all modes have real freqencies. In fact, each of Landau's
solutions is a superposition of infinitely many true modes, and damps as
these drift out of phase.
Van Kampen showed that the true modes have two remarkable features:
(a) they
have singular wavefunctions, (i.e., ones that involve a
The situation as regards the normal modes of self-gravitating systems is
only now emerging from the work of
Mathur (1990),
Weinberg (1991),
Louis (1992),
and others. Spatially limited gravitational systems differ from the
classical electrostatic plasma in that there is an upper bound on the
dynamical time of any of its constituent particles, namely the time to
complete a circular orbit around its periphery. If the entire system
pulsates with an even longer period than this, no particle will be in
resonance with the pulsation, and the latter will not be damped by loss of
energy to resonant particles. (The singularity of Vlasov's integrand, and the
damping of Landau's solutions arise precisely from the inevitable presence
in a plasma of resonant particles.)
Whenever a gravitational system is capable of oscillating with a
period longer than that of any particle, (2)
the system will have a discrete normal mode.
For example, the Hunter & Toomre criterion,
As the structure of a stellar system is made more centrally concentrated,
the range spanned by its particles' frequencies broadens and the ``gap''
between zero frequency and the lowest particle frequency shrinks. As the
upper boundary of the gap moves towards zero it engulphs and destroys
successive discrete modes. But
Louis (1992)
finds that if the boundary has
not long swallowed a mode, it is usually possible to detect in n-body
simulations an oscillation very much like the swallowed mode. These relic
oscillations do not simply decay like Landau's solutions, but fluctuate in
amplitude, presumably in step with the transfer of energy from pulsation to
resonant particles and back again.
To date this improved understanding of low-frequency oscillations of stellar
systems has not been applied to the bending modes of disks. But it does make
one wonder whether disks may not have rather long-lived warped
configurations which are neither discrete modes nor the exponentially damped
waves studied by Landau. Probably more effort should be given to studying
the initial-value problem for disks made up of N rings, since
this probably behaves less subtly in the limit N -> 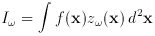
 is a
continuous function of
is a
continuous function of  ,
I
,
I will be one too.
So any plausible excitation mechanism will excite all modes with frequencies
in some interval, and will thus launch a wave-packet. Since the frequencies
of these modes differ slightly from one another, their relative phases will
evolve in time, and the packet will gradually disperse.
will be one too.
So any plausible excitation mechanism will excite all modes with frequencies
in some interval, and will thus launch a wave-packet. Since the frequencies
of these modes differ slightly from one another, their relative phases will
evolve in time, and the packet will gradually disperse.
 -function),
and (b) they do not satisfy a dispersion relation
-function),
and (b) they do not satisfy a dispersion relation  (k). Rather for
every pair (
(k). Rather for
every pair ( , k) there
is a van Kampen mode. Evidently the limit
N ->
, k) there
is a van Kampen mode. Evidently the limit
N ->  for a
collisionless system of N particles has to be treated with some care.
for a
collisionless system of N particles has to be treated with some care.
 dR /
dR /  (R) <
(R) <  , for
the existence of a discrete mode, ensures that
there is negligible mass in particles with z-frequencies as low as the
pattern speed.
, for
the existence of a discrete mode, ensures that
there is negligible mass in particles with z-frequencies as low as the
pattern speed.
 than do the system's normal modes.
than do the system's normal modes.
2 Strictly, as
Louis (1992)
points out, the criterion must be formulated in a way which takes into
account any selection rule between mode and particle such as may be imposed
by considerations of parity.