Athanassoula et al. (1987) introduce criteria from spiral structure theory, and in particular those for swing amplification (Toomre 1981), in order to get limits on the dynamical importance of the disc. Since observed discs are usually bisymmetric, it seems natural to ask for the possibility to have amplification of m = 2 structures, which imply a minimum for (M / L)disc. On the other hand, one would like to suppress m = 1 structures, which implies an upper limit for (M / L)disc. This limit usually coincides with the requirement to have ``maximum discs'' but with halos with non hollow cores. Athanassoula et al. (1987) find that these latter models are preferred when considerations of stellar populations and the buildup of Sc discs at a constant rate of star formation over a Hubble time are taken into account.
| 
|
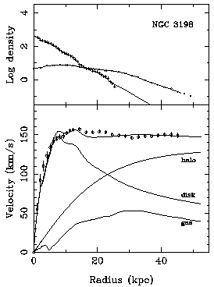
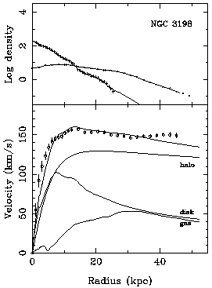
Figure 1. Mass models for NGC 3198. At left a ``maximum disc'' model, at right a ``no m = 2'' model. Data from Wevers et al. (1986) for the photometry, and Begeman (1989) for the rotation curve. A Hubble constant of 50 km s-1 Mpc-1 is assumed. | |
The way this works is illustrated in Figures 1
and 2 for the galaxy
NGC 3198. For the swing amplifier to work, we need
several quantities
which depend on the rotation curve. These are the parameters 
and X, given by :
where
As can be seen, the active disc mass, µ, comes in, as well as
the number of arms, m. The rotation curve is also represented via the
epicyclic frequency,
Athanassoula (1984)
rediscussed the swing mechanism presented by
Toomre (1981),
and calculated for various values of
Figure 2. Curves of
For NGC 3198, it is clear that the ``no m = 2''
criterion leads to
a disc rotation curve whose maximum velocity is 105 km s-1.
This can be compared to the value of 100 ± 19 km s-1
derived by
Bottema (1993)
from his criterion based on his velocity dispersion
work, and also by the maximum values of 93 and 100 km s-1
calculated by
Navarro (1998)
for his models, which are partly based
on notions from cosmological simulations, and include tacitly that
the adiabatic compression of the halo material due to the disc
formation is functioning as predicted. While the Bottema
criterion is still in rough agreement with the swing amplifier
criteria given the uncertainties, the models of
Navarro (1998)
are not anymore : for them the disc is just a bit too light to allow swing
amplification of m = 2 structures.
In conclusion, the method used by
Athanassoula et
al. (1987)
gives a range of values for the mass-to-light ratio of the
disc, with the upper limit very often close to or identical with
a ``maximum disc with no hollow core halo'' solution, and a lower
limit which is higher than the values current fashionable arguments
from cosmological simulations seem to advocate.
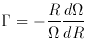
is the dimensionless
shear rate. This quantity is 1.0
for exactly flat rotation curves, 1.5 for Keplerian curves and 0.5 for
a curve rising as the square root of the radius. The other quantity is
.
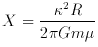
the
maximum growth factor of the swing amplification as function of
X for 3 typical values of the Toomre parameter Q.
In Athanassoula et
al. (1987)
we use an interpolation method
to determine the amplification factor for any value of and X.
As a result, we can for a given mass model work out its consequences
for the amplification of m = 1, 2, 3, ... structures, and calculate
graphs such as presented in Figure 2. It can be
easily seen from Figure 2 that if we lower the
mass-to-light ratio of the disc with
a factor 2, the curves for m = 2 become those in the top panel, and
the curves for m = 4 those in the middle panel (since mµ is
what matters).
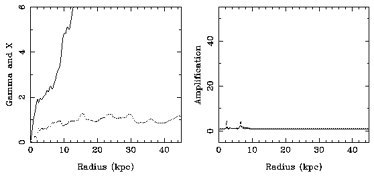
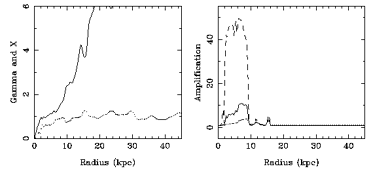
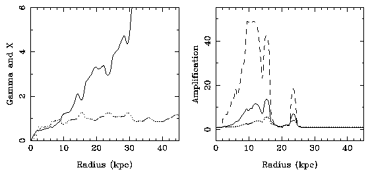
(dotted line) and X (continous
line), at left, and the maximum
amplification for three values of Q (Q = 1.2 : dashed line, Q = 1.5
: continuous line and Q = 2.0 : dotted line), at right, for the
``maximum disc'' model of NGC 3198 shown in
Figure 1. At the top,
the results for m = 1, in the middle, the results for m = 2, and
at the bottom, the results for m = 4.