3.6.2. Virgocentric Flow

Shortly after the detection of the DA, Aaronson et al. (1980) presented evidence that the determination of H₀ from the distance and observed velocity of the Virgo cluster yielded systematically lower values than using more distant clusters. This difference suggested that the observed velocity of Virgo was not equal to its cosmic velocity but instead was a combination of its cosmic velocity and the infall of the Local Group towards Virgo. This phenomenon is known as Virgocentric flow. A schematic illustration of the way that a virialized structure like Virgo perturbs the local Hubble flow is shown in Figure 3-16. Virgocentric flow seriously distorts the relation between redshift and distance as multiple distances can give rise to the same observed velocity.

Figure 3-16: Distortion of the Velocity Field which is caused by spherically symmetric infall into a virialized structure. Here the spatial distribution of infall galaxies is plotted with heads or tails on them to indicate the amplitude of their infall velocity. Note that the heads and tails always point at the center of the virialized cluster. This figure comes from Villumsen and Davis (1986).

Let's assume for the sake of illustration (and easy math) that the distance to Virgo is 15 Mpc and that H₀ = 100. The cosmic velocity of Virgo is then 1500 km s^-1. A galaxy in Virgo at this distance which was at rest with respect to the Virgo cluster would also have a velocity of 1500 km s^-1. However, a galaxy located at a distance of 10 Mpc between us and Virgo could be accelerated by Virgo to a velocity of 500 km s^-1 and thus its observed velocity would be 1000 + 500 = 1500 km s^-1 even though its distance is 10 Mpc. Similarly, a galaxy located at 20 Mpc could have its expansion velocity with respect to us retarded by its proximity to Virgo at a value of 500 km s^-1 and hence its observed velocity would be 2000 - 500 = 1500 km s^-1. To understand that this was occurring would require the measurement of relative distances with sufficient accuracy that could resolve the differences between distances of 10,15 and 20 Mpc.

If Virgo is intrinsically at rest with respect to the CMB, then a determination of the Milky Way's infall velocity will provide the necessary correction to the observed velocity of Virgo to produce its cosmic velocity. From this cosmic velocity, H₀ can be determined using the Virgo cluster distance modulus determined in the last chapter. Significant efforts to determine this infall velocity were made by Aaronsonet al. (1982) and Davis and Peebles (1983). Those efforts continue to the present day with no real convergence on the infall velocity. Values of 250 (Aaronson et al. 1982; Jerjen and Tammann 1992) - 350 km s^-1 (Tonry et al. 1993) are consistent with the data and this range of values produces a 10% error in the determination of H₀ even if we know the distance to the Virgo cluster with arbitrary accuracy.

This infall of the Local Group towards Virgo should also be reflected against some more distant reference frame. In 1986, Aaronson et al. were able to detect this reflex motion of the LG using a reference sample of clusters located at distances of 50 - 100 Mpc. Moreover, this detection also carried with it one of the initial indicators that the scale over which peculiar velocities are generated is significantly larger than the separation between Virgo and the LG. As discussed earlier, the DA does not point directly at the Virgo cluster. The vector difference between the DA and the Virgo cluster points in the general direction of the Hydra-Centaurus region. This suggests that the Local Supercluster is feeling the attraction of its nearest mass concentration, the Hydra-Cen Supercluster. This situation is schematically illustrated in Figure 3-17 and shows that Virgo itself may also be moving.

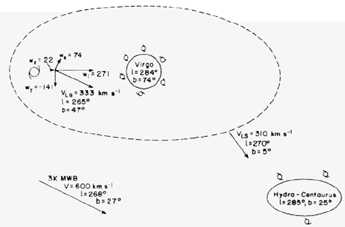
Figure 3-17: Schematic representation of the Local Velocity Field from Aaronson et al. (1986). Here the Milky Way is infalling towards Virgo at approximately 300 km/s and the entire local Supercluster is infalling towards Hydra-Cen at approximately 300 km/s. The vector sum of these two infall components to the motion of the Milky Way approximately accounts for the observed dipole anisotropy in the CMB.

Thus, a correction for Virgocentric Infall alone is insufficient to recover the cosmic velocity of Virgo. An additional correction for the motion of the entire Local Supercluster towards Hydra-Cen must now be formulated and applied. In a kinematic description of the local velocity field, the motion of the LG towards Virgo can be thought of as a form of dipole anisotropy. The influence of Hydra-Cen acts as a quadrupole anisotropy in the local velocity field. (see for instance Lijle et al. 1987). If mass concentrations other than Hydra-Cen are felt by the LG then higher order anisotropies need to be considered as well.