3.9. A Determination of H₀ Using the Virgo and Coma Clusters

The identification of large scale peculiar velocities is a potentially serious obstacle to the recovery of H₀ from local samples of galaxies. In fact, Turner et al. (1992) suggest that could be fatal and make the possibly prophetic remark that

Even if the local expansion rate is known to be 80 ± 8 km/s/Mpc out to 30 h^-1 Mpc in the North Galactic Cap, the 95% confidence limits on the true global value of H₀ is 50-128 km/sec/Mpc in a CDM model.

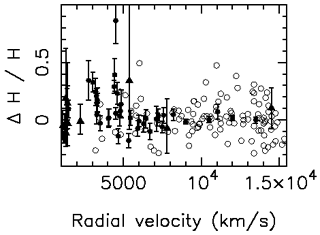
To counter this with observations Mould (1996) has developed a simple but effective model which assumes that H₀ is 50% higher when measured using a local sample of galaxies compared to using samples that are located at the distance of the Coma cluster or beyond. Figure 3-23 summarizes the data used in comparison with the model. Although the data are noisy (due both to errors in distance estimates and to peculiar velocities), the mean value reaches H / H = 1 by v 7000 km s^-1. This strongly suggests that a global value of H₀ can be recovered by using samples of galaxies at these distances or by accurately measuring the relative distance modulus between Virgo and Coma. We now proceed to do exactly that but first we demonstrate why using the Virgo cluster alone is not the ideal route for determining H₀.

Figure 3-23: Deviations from a uniform Hubble flow compiled by Mould (1996). Solid circles: clusters of galaxies with Tully-Fisher distances. Solid triangles: EPM data of Schmidt et al. (1994). Open symbols: brightest cluster members from Lauer & Postman (1994). There is no evidence that a significantly different value of the Hubble Constant pertains for samples located inside and outside the distance of the Coma cluster at v = 7200 km/sec. Moreover, it is clear that beyond 5000 km/s, the noise in determining H0 has greatly diminished. Note the considerable scatter in the Lauer and Postman sample.

The first step in this process is to determine the cosmic velocities of Virgo and Coma. The observed velocity of Virgo is determined in the heliocentric frame of reference, that is the velocity with respect to the Sun. Since the sun is rotating around the galaxy, then a correction for galactic rotation must be done so that the Virgo velocity is with respect to the Milky Way galaxy. In addition, there is a small correction for the random perturbation on the Milky Way galaxy produced by the other LG members. Both of these corrections are well understood and the transformation from heliocentric to galactocentric velocity is

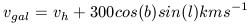
(40)

where b and l are coordinates in galactic latitude and longitude. The cosmic velocity of Virgo is then

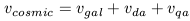
(41)

where v_da represents the dipole term in the local velocity field (essentially the pattern speed of infall of the LG towards Virgo) and v_qa is the quadrupole term that represents the random effects of other mass concentrations on Virgo's motion. Unfortunately, as previously discussed, current determinations of v_da and v_qa are rather uncertain and certainly model-dependent.

In addition, it is now generally recognized that the Virgo cluster has substantial substructure (see Yasuda et al. 1996) which makes the determination of the mean v_h somewhat problematical. For instance, v_h for M87, the brightest and most massive galaxy in Virgo is 1292 ± 10 km s^-1. But the mean velocity of all probable members of Virgo (some 700 galaxies with velocities) is v_h = 1150 ± 51 km s^-1. All of this translates into a rather large uncertainty in v_cosmic for Virgo and this does not seem like a promising route to take to recover H₀.

The better way to determine v_cosmic is to use v_cosmic for Coma and measure the relative distance between Virgo and Coma. Since Coma is only a few degrees away from Virgo in the plane of the sky, then our radial infall towards Virgo is reflected in the observed velocity of Coma. However, since the observed velocity of Coma is 7000 km s^-1, an uncertainly of ± 100 km s^-1 in our Virgocentric infall velocity is rather inconsequential. Several hundred velocities have been measured for galaxies in the Coma cluster core and the resulting mean velocity is v_h = 6925 km s^-1. If we use an infall velocity of 300 ± 100 km s^-1 then we derive v_cosmic = 7225 ± 100 km s^-1.

The relative distance modulus between Coma and Virgo has been measured by a number of different techniques and the agreement is good. The most credible methods and results are the following:

The H-band TF measurements of Aaronson et al. yield (m - M) = 3.69 ± 0.16. There is some concern that many of the spirals used in the sample of Aaronson et al. are not associated with small foreground and background groups and not with the Coma cluster. Indeed there is some evidence (e.g., Bothun et al. 1992) that spirals are currently infalling to Coma as they are to Virgo. However, the Aaronson et al. sample is not biased towards preferential sampling of the front side of Coma but instead has sampled over the entire range of possible infalling galaxies.

Using the Color-Magnitude relation for Ellipticals as measured in the UBV passbands, Sandage (1972) derives (m - M) = 3.66 ± 0.14. The relation between color and intrinsic luminosity for ellipticals is likely driven by metallicity variations as a function of the stellar mass of the elliptical. The metallicity of a star determines its atmospheric opacity at different wavelengths. This is especially true in the case of the atmospheres of Red Giant stars whose light dominates that of elliptical galaxies. The CM effect is better measured in the infrared than the optical and IR observations by Bower et al. (1992) yield (m - M) 3.70 ± 0.09.

The D_n- relation as applied by Dressler et al. (1987) yields (m - M) = 3.65 ± 0.20. Evidence that Virgo and Coma elliptical define the same intrinsic D_n- relation has been presented by Lucey et al. (1991).

From these methods, a mean Virgo - Coma relative distance modulus of (m - M) = 3.68 ± 0.03 results. This is an extraordinarily small error bar which reflects the overall consistency of relative distance determinations. This relative distance modulus assumes there to be no foreground reddening towards either Virgo or Coma. The Coma cluster is very near the galactic north pole and Virgo is also at fairly high latitude, so E(B - V) = 0.0 seems reasonable.

It would now seem that we are in a reasonable position to derive H₀. A relative distance modulus of (m - M) = 3.68 corresponds to a factor of ((10^{0.40 (m - M)}))^1/2 = 5.45 in linear distance. The predicted v_cosmic for Virgo is then 7225 / 5.45 = 1326 ± 25 km s^-1. The low error bar indicates that the uncertainty in LG infall velocity is no longer very important when v_cosmic is derived in this manner. From the last chapter we saw that the most probable distance modulus to Virgo was in the range (m - M) = 30.9 - 31.2 or linear distances of 15.1 - 17.4 Mpc. The lowest value of H₀ that can be obtained is 1351/17.4 = 78. The highest value of H₀ that can be obtained is 1301/15.1 = 86. Placing Virgo at a distance of (m - M) = 31.5 yields H₀ = 68. We thus conclude a firm lower limit of 70 can be placed on H₀. A likely upper limit is 90 which is achieved using (m - M) = 30.8. This is the distance that results if the distance to LMC is (m - M) = 18.35. It is our prediction that more precise determinations of H₀ will converge on values between 70 and 90. For a range of of 0.1 - 1.0, this range in H₀ produces a range in expansion ages of the Universe of 7.5 - 13.5 billion years. This seems to be significantly less than the age of the oldest stars in globular clusters. Such an age range leaves the door wide open for non-zero cosmologies and this may be the most significant result that has been obtained after 30 years of searching for the value of H₀.