4.6.3. Nucleosynthesis Constraints on Baryonic Matter

There appears to be no single baryonic candidate that can dominate the halo mass of our Galaxy and escape local detection. Undoubtedly, baryonic dark matter exists in the form of cool white dwarfs and very low mass stars (e.g., brown dwarfs) but the space density of both those populations is unknown. Available data are consistent with there being as much mass density in these objects as existing stars, but certainly not 10 times more. There are also significant constraints on the total number of baryons in the Universe that come from the observed abundances of the light elements ³He, ⁴He and ⁷Li. There are two competing theories for the production of light elements in Big Bang nucleosynthesis:

1. The homogeneous model: This assumes a homogeneous universe with rather small lepton number. This is important as the early exchange of neutrons to protons and vice-versa is mediated by neutrinos (leptons).

2. The inhomogeneous model: This assumes that during the quark-hadron phase transition (at early times, the universe was sufficiently small and quarks were so close together so as to overcome the mediating force of any gluons. Hence quarks were not found in hadrons but instead were free. As the universe expands and cools, these quarks must get bound inside hadrons) there were induced density inhomogeneities that produced regions of excess neutrons.

The inhomogeneous model was studied in much detail in the late 80s because with a sufficient density contrast and a short enough length scale for neutron diffusion, some models suggested that the observed baryon abundance could be made consistent with an = 1 baryon-dominated universe. If these models were correct, then this would strongly motivate the general acceptance of the inflationary paradigm but at the same time would beg the question "Where are all these baryons?", which, coincidentally is the subject of Chapter 6. Inhomogeneous nucleosynthesis models became a small cottage industry of the late 1980s (Alcock et al. 1987; Kurki-Suonio et al. 1990) and each model had its own unique diffusion process between the neutron-rich and proton-rich sites. This cottage industry was effectively shutdown in the early 90s as better developed theory of quark-hadron phase transition showed it to be a second order instead of a first order phase transition thus leading to much lower levels of inhomogeneity (see Olive 1991; Goyal et al. 1995).

Under the homogeneous model, the abundance of light elements depends primarily on the baryon-to-photon ratio . This ratio remains unchanged after the final set of e⁺e^- annihilation occurred in the first 10 seconds. The abundance of light elements depends on since the formation of ³He requires a seed population of Deuterium (²H). If is sufficiently high then ²H will be photodissociated before it can fuse with another proton to form ³He. In contrast, if is too low, then in the expanding universe there won't be a sufficient density of protons for the newly formed ²H to find and there would be very little Helium production. We define the baryon density as _b and its contribution to the total mass density of the Universe as _b = _b / _c. Recall that _c = 3H² / 8 G and hence

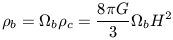
(25)

The determination of the abundances of light elements has been a subject of much research. The best astrophysical locations which have been investigated are the atmospheres of metal poor stars and meteoritic material. It is also possible to directly detect interstellar or intergalactic deuterium in the UV although the strength of Deuterium is 10^-5 that of Lyman. A possible detection of Deuterium towards a distant QSO was reported in some HST observations by Hogan et al. 1995 although distinguishing that line from the myriad of QSO Lyman lines at different redshifts is difficult and so this detection is not secure (see also Tytler et al. 1997). The most recent constraint or limit on _b comes from a large and comprehensive analysis by Walker et al. (1991) who derive

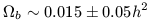
(26)

For an h = 1 (H₀ = 100) _b lies in the range .01 - .02. Recall that for luminous stars was 0.005 and hence equation 26 leaves ample room for baryonic dark matter at a level up to 4 times that of the mass contained in luminous stars. For h = 0.5 (H₀ = 50) _b could be as large as 0.08. As previously mentioned in Chapter 3, there is good evidence that we also have a "missing" baryon problem. This is discussed in more detail in Chapter 6.