5.1.3. Stability Criterion

Our goal is to turn this self-gravitating fluid in to a galaxy and to furthermore do this in an expanding universe. Let's first consider the situation in a static medium. We assume that the fluid is initially in a state of equilibrium that satisfies our three equations, namely,

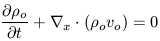
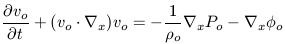
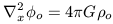
We give a small perturbation to this fluid which causes it to deviate from the equilibrium state. If this fluctuation merely damps out then the equilibrium is restored and nothing interesting happens. On the other hand, if the perturbation causes the non-equilibrium state to amplify with time, then the initial perturbation continues to grow without limit. If the pressure, density and velocity in the fluid are such that it is stable, then all perturbations will eventually decay to zero. The technique of linear perturbation analysis allows each instant of the fluids' evolution to be described as the superposition of two separable components - one which corresponds to the equilibrium state and the other that corresponds to the perturbed state. The key simplification is to consider arbitrarily small perturbations such that the perturbed state is very close to the equilibrium state. This allows us to write the density, pressure, velocity and gravitational potential of the perturbed state as follows

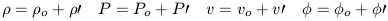
(6)

In all cases, the perturbed quantities (denoted by ') are very much smaller than the initial quantity. To further simplify the physics, we apply the reasonable demand that all perturbations in the fluid involve no energy gain or loss, only changes in density, pressure and velocity. Thus, we assume these perturbations to be adiabatic.

We now substitute our expression for the perturbed density into the equation of continuity to yield:

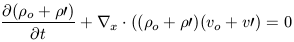
(7)

Expanding out the terms yields

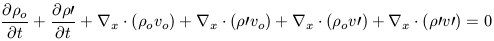
Since the ' quantities are very small, then the product ' v' is vanishingly small and can be dropped. In addition, the purely equilibrium terms cancel and we are left with:

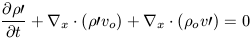
(8)

Linear perturbation theory thus produces an equation which is linear in all the surviving terms. We can apply the same technique to Euler's and Poisson's equation to yield:

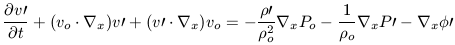
	(9)
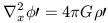
	(10)

The equations presented here were first derived by Jeans. His solution was to assume a uniform and static fluid in which v = v₀ at all times and hence and P are constants. However, Euler's equation indicates that this condition can only be satisfied if ₀ = 0; a condition that, by Poisson's equation, requires ₀ = 0. Hence, for the case of a static fluid it is only possible to satisfy the equilibrium equations if we have the unphysical situation that ₀ = 0. This means that no equilibrium state is even possible for a static, self-gravitating fluid.

Yet, it is clear that perturbed fluids can only be understood in this frame work if we have the condition of ₀ = 0. Jeans resolution to this dilemma was to apply some physical insight to simplify the mathematics by assuming that the gravitational field which originates from the unperturbed state can be ignored and hence the self-gravity of the fluid is determined only by the perturbed component. This assumption, known informally as the Jeans Swindle, has the most validity in the case of an infinitely long, uniform fluid. In this case, any dynamic evolution in the fluid is uniquely determined by the self-gravity associated with the perturbed state. If we now set v₀ = 0, ₀ = constant, P₀ = constant and ₀ = 0 the linearly perturbed fluid dynamics equations become

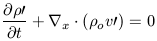
	(11a)
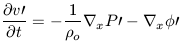
	(11b)
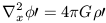
	(11c)

The time derivative of equation 11a is

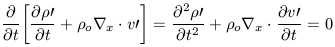
(12a)

and the divergence of equation 11b is

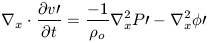
(12b)

This gives us the term ² which appears in Poisson's equation. Equations 12a and 12b can now be combined to yield:

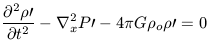
(13)

This second-order partial differential equation fully describes the time rate of change of the small density perturbation, '. This time rate of change competes with the contribution of pressure gradients and changes in the gravitational potential. Hydrostatic equilibrium (ð² ' / ðt² = 0) is recovered from this framework if the pressure and gravity terms exactly cancel each other. The physical importance of equation 13, however, lies in the fact that density perturbations (e.g., ') require increasingly larger pressure gradients to stabilize them against further amplification. Equation 13 specifies the conditions for an effective runaway process which allows the density perturbation to continue to grow. Amplification of the density perturbation, however, requires that the perturbation travels through the fluid medium at some characteristic speed. We can easily derive this characteristic speed by ignoring the effects of gravity. In this case

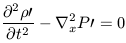
(14)

This equation has two unknowns (' and P') which are related to each other via the equation of state of the fluid. Since our fluid is really hydrogen gas in the early Universe, its is reasonable to use the ideal gas law:

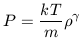
(15)

where k is Boltzmanns constant, T is the temperature of the gas, m is the mass of an individual particle in the gas and = 1 for an isothermal gas or 5/3 for an adiabatic one. In this formulation, density increases lead directly to increases in pressure which push outward to smooth out any density inhomogeneity. This pressure exerts a force on regions that surround our fluid element causing their density and pressure to increase. In this manner a "pressure wave" propagates through the fluid as individual fluid elements are coupled to one another. This pressure or acoustic wave propagates at a characteristic speed, the sound speed c_s. The sound speed is directly related to the rate of change of pressure with density at constant entropy. For an ideal gas law, the sound speed is defined as c_s² ðP / ð. From equation 15 we have

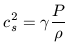
(16)

We substitute this into equation 14 to yield what looks very much like a classical wave equation:

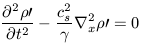
(17)

In the absence of gravity, small density perturbations will lead to small pressure perturbations that propagate through the fluid like a wave. In essence, this leads to variations in density through the medium that also propagate in the x direction like a wave and can be described as

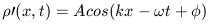
where A is the amplitude of the wave, is the frequency and k is the wave number of the oscillation where k is defined as 2 / , and is the phase of the wave. In general, A can be identified with the initial density enhancement and can be set to zero by the proper choice of coordinates. Furthermore, c_s is related to k and via the familiar dispersion relation for waves:

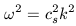
If we consider the effects of gravity via the same plane wave analogy an additional term appears in the dispersion relation:

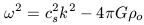
(18)

This equation now specifies the behavior of the fluid in different physical limits. At very high wavenumbers (very short wavelengths) gravity can be effectively ignored and the physics reduces to that of the acoustic wave behavior we obtained previously. In this case, the perturbation oscillates without energy dissipation until its damped out by viscosity and/or friction. In the very early Universe, radiation and matter are coupled such that photons become a significant source of viscosity that effectively prevent the growth of short wavelength perturbations. This would lead to a characteristic length scale below which structure should not form.

Gravity, however, does dominate in the limit of very long wavelength perturbations, in which case the pressure terms become unimportant. In this case, ² becomes negative and requires a solution which is a complex number. The simplest form of this solution is ² = -b. For this solution, the density perturbation has a time dependence which goes as

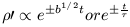
(19)

where is the e-folding time over which the perturbation grows or decays,

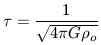
(20)

We have now derived the general result that very long wavelength density perturbations in the fluid will have an amplitude that grows exponentially in time and that this growth rate is inversely proportional to the square root of the initial fluid density. This result should be intuitive. Denser perturbations have more self-gravity associated with them and hence can drive the instability at a faster rate. It then follows that there must be some critical length scale, _j which defines the boundary between perturbations that damp out from those that amplify exponentially. This critical value is known as the Jeans length which is defined as

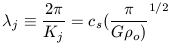
(21)

or alternatively, for a spherical perturbation of diameter _j the Jean's mass is

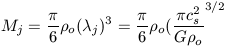
The only physical parameters in this characterization are c_s and ₀. Since c_s is essentially a measure of the pressure in the fluid, then the Jeans criterion for gravitational collapse is a direct competition between internal pressure and external self-gravity. Since gravity is largely a volume effect then this analysis implies that on larger scales, self-gravity will ultimately exceed pressure. This of course, is the physical premise behind star formation in molecular clouds. As we will see shortly, the main physical difference with respect to galaxy formation is that this criteria must be established in an expanding Universe in which the density is constantly dropping. Note also that since pressure is proportional to temperature, a larger Jeans mass is required to overcome the internal pressure for high temperatures. This essentially precludes any possibility of structure formation at early times when the temperature is high.

High temperature also means very high radiation pressure. As the matter is coupled to this radiation, the matter experiences radiation drag and is redistributed in a manner which is the same as the distribution of the radiation. The CMB observations show that the radiation is distributed nearly homogeneous. Clearly, if the matter distribution ends up to be completely homogeneous then there is no net gravity and no structures can form. Hence, density inhomogeneities must be maintained throughout the radiation dominated era in order that structure can form in the matter dominated era. These density enhancements in the matter produce the Sachs-Wolfe effect discussed earlier. COBE has now measured the overall amplitude to be 1.5 x 10^-5. Can such a minute density enhancement actually be amplified to produce structure? The answer is, easily, because of the exponentially growing nature of the fluctuation.

Let's consider the case of a modest galaxy with total mass 10¹¹ M. If we assume this object is initially composed only of hydrogen gas then there are 10⁶⁸ atoms involved. Purely random fluctuations (which go as 1 / N) in the initial distribution of atoms would then lead to a random density fluctuation of ₁ / ₀ 10^-34. After 80 e-folding times, this almost negligible density perturbation would have grown to _{1 0}. By 100 e-folding times this perturbation would grow to ₁ 10⁴ ₀ which is about the current ratio of the average density of a galaxy to that of the Universe. Suppose that we start growing this perturbation after recombination has occurred and the Universe is no longer ionized. At this redshift (z 1100), the average density of the Universe is 10^-18 g cm^-3 leading to an e-folding time of 10⁴ years, ample time for the perturbation to grow. The fallacy of this argument is that the Universe is expanding and thus is steadily decreasing resulting in an increase in . This means that the growth rate of perturbations in an expanding universe is considerably slower than the case of a static medium.

There is an additional complication. Galaxies are not mildly overdense structures but instead have a density contrast of 10⁴ - 10⁵. Galaxies are hence highly non-linear structures which means that linear perturbation theory breaks down long before the process of galaxy formation is complete. This non-linearity occurs on larger scales as well. For instance, a typical cluster of galaxies has a density contrast within R 1 Mpc of 200 and even a supercluster of galaxies, in scales of 5-10 Mpc, is overdense by factors of 10-20. As the observed structure in the Universe is strongly non-linear, this means that growing gravitational perturbations rapidly cross into the non-linear regime thus nullifying the original premise of small perturbations.

To determine the physics of what happens when this boundary is crossed requires an understanding of the very complex theory of non-linear perturbations. A chief feature of non-linear perturbations involves non-linear partial differential equations which contain important cross terms that relate to the coupling of perturbations at different wavelengths. Recall that in linear perturbation theory, there is no coupling. This mode coupling likely plays a crucial, but largely unknown role, in the advanced physical development of these instabilities. Currently, these effects are best studied via large N numerical simulations. Analytical descriptions of the process remain fairly opaque and certainly beyond the level of this book. This doesn't mean that linear theory is without merit, however, as clearly a necessary condition for the growth of perturbations via non-linear processes is the existence of perturbations on some-scale which have ₁ / ₀ 1. Hence, linear perturbation theory should continue to be an adequate description of the initial growth and development of the perturbations that have evolved to produce the observed structure. Our difficulty with non-linear effects then suggests that the formation of smaller-scale structure (e.g., galaxies) may be much more difficult to describe than the formation of the largest scale, lowest-density features that we observe.