5.1.7. Numerical Games with the Jeans Mass

Recall that the Jeans mass at anytime in the Universe is a function of its temperature and density. For our case of an ideal gas, the Jeans mass for a spherical perturbation is

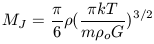
It is interesting to calculate then what M_J is at recombination to see if that corresponds to any known astrophysical objects. Recombination occurs at z 1100. The temperature of the Universe scales as (1 + z) so if its 2.7K currently then it was 3000K at recombination. The density scales as (1 + z)³. The current density of the Universe is in the range = 10^-29 - 10^-30 or = 10^-20 - 10^-21 at recombination. The lower range of values would correspond to a very open Universe and the upper range is the approximate density in an = 1 model (recall that _crit depends on H₀). For this range of current densities, M_J is 1-4 x 10⁵ M. This mass is very similar to the masses of globular clusters, which are known to be the oldest collections of stars in the Universe. There are many that think this is just a coincidence, but from a physics point of view, we have the logically consistent argument that objects with mass a few times 10⁵ M could collapse under their own self-gravity following recombination. Since the Jeans Mass is a minimum mass, then it is also clear that galaxies (10¹¹ M) and cluster (10¹⁵ M) size perturbations are far above the Jeans criteria so that pressure can be ignored.

If we measure the present day densities of globular clusters, galaxies and clusters of galaxies, we find a sequence of progressively decreasing density. Since the dynamical timescale of a density enhancement goes as (G )^-1/2, then these dense, globular cluster mass perturbations collapse the first. Although its difficult to guess the initial size and density of these perturbations, we can make a rough estimate of how fast they could have collapsed. If our galaxy size perturbation of mass 10¹¹ M had an initial radius of 50 kpc then the initial density would be 2 x 10^-25 g cm^-3 leading to a dynamical timescale of 300 million years. At z = 10, the Universe is approximately 3% of its present age meaning that their is time for a galaxy size perturbation to have gravitationally collapsed by this redshift. The halo parameters deduced by Zaritsky et al. (1996) lead to a collapse time approximately twice as long as this case. In the next chapter, we will introduce the properties of a newly discovered population of galaxies known as Low Surface Brightness galaxies. These galaxies appear to be up to 100 times lower in mass density than normal galaxies and hence would represent galaxy size perturbations which have long collapse times and late formation. In fact, its important to emphasize that any range of matter densities in protogalaxies, at fixed mass, produces a range of collapse times and formation epochs.

At the smallest scale are Globular clusters which range in mass from 10⁵ - 10⁶ M over a scale size approximately 1000 times less than a typical galaxy. This leads to a density which is 10⁴ times that of a galaxy. Hence their dynamical timescales are only a few million years at most and they easily could have formed by z = 100. Extremely dense globular clusters would have formed even earlier and could be subject to some interesting dynamical evolution that might lead to the formation of gamma ray burst objects (discussed in Chapter 6).

At the other size scale, a cluster of galaxies will have a significantly longer collapse time. Although these structures have 10³ - 10⁴ times more mass than a galaxy, their scale sizes are at least 100 times larger. Hence the overall density is down by two orders of magnitude which yields to an order of magnitude longer collapse times. We therefore would not expect to find clusters of galaxies at high redshift. For a 15 billion year old Universe and an average collapse time of 3 billion years, we would expect no clusters to exist beyond redshift z 2.