

© CAMBRIDGE UNIVERSITY PRESS 1997
| |
1.2 Thermal and Non-Thermal Processes
During the pioneering stage of radio astronomy, as a wide range of celestial objects turned out to be detectable in the radio spectrum, the two broad classes of emitter became clearly distinguished. At centimetric wavelengths the radio emission from the Sun, as observed by Southworth (see Appendix C), could be understood as a thermal process, with an associated temperature. The term temperature implies that there is some approximation to an equilibrium, or quasi-equilibrium, condition in the emitting medium; in this case the medium is the ionized solar atmosphere. The mechanism of generation is electron-ion collisions, in which the radiation is known as free-free emission or bremsstrahlung. At metre wavelengths, however, the outbursts of very powerful solar radiation observed by Hey (Appendix C) could not he understood as the result of an equilibrium process. The distinction was therefore made between thermal and non-thermal processes, a distinction already familiar in other branches of physics. Many of the most dramatic sources of radio noise, such as the supernova remnants Cassiopeia A and the Crab Nebula, the radio galaxies M87 and Cygnus A, and the metre-wave backgrounds from our own Milky Way Galaxy, are non-thermal in nature.
Nevertheless, for practical reasons the term ``temperature'' was adopted in a variety of contexts, following practices that had been used widely in physics research during the 1940s. Within a system, individual components can exhibit different temperatures. In a plasma excited by a strong radio-frequency field, for example, the electron and ion components of the gas may each show velocity distributions that can be approximated by Maxwell-Boltzmann distributions, but at quite different temperatures. Each component is in a state of approximate thermal equilibrium, but the systems are weakly coupled and derive their excitation from different energy sources. One can speak, therefore, of two values of kinetic temperature, the electron temperature and the ion temperature.
A two-state system such as the ground state of the hydrogen atom, in which the proton and electron spins can be either parallel or antiparallel, can be used as a simple and illuminating example of how the temperature concept can be generalized. Given an ensemble of identical two-state systems at temperature Ts, the mean relative population of the two states, <n2 / n1>, is given by the Boltzmann distribution
where the energy separation
The state temperature need not be positive. When <n2 /
n1> is greater
than 1, Equation (1.1) requires a negative state temperature, and this
is precisely the condition for maser or laser action to occur. Whereas a
resonant photon beam traversing a medium at a positive state temperature
suffers absorption, it will be amplified if the state temperature is
negative. Naturally occurring masers are common in astrophysics,
particularly in star-forming regions and in the atmospheres of red
giants. These are treated in Chapters 7 and 9. The population inversion
is maintained by a pumping mechanism, which can either be radiative or
collisional, but whose action may be to fill the upper state faster than
the lower state, or to populate both states, but with the lower state
being drained of population more rapidly.
Atomic and molecular systems almost always have a large number of
bound states, and one can associate a state temperature with each pair
of states. If the system is in a state of thermal equilibrium, all these
temperatures will be the same. The case of blackbody radiation, which is
an example of a system with a continuum of energy states, is treated in
Chapter 2 and the idea of brightness temperature is introduced. In
brief, this assigns to an emitter of radiation at frequency v the
temperature that it would have to have if it were a black body. This
need not correspond to a physical temperature, and the powerful
non-thermal emitters exhibit brightness temperatures that can exceed
1012 K. Conversely, a thermal source of radiation need not have a
brightness temperature that is constant over a wide spectrum and equal
to the physical temperature; the variation of brightness temperature
with frequency will be determined by the equation of radiative transfer,
introduced in Chapter 7.
The temperature concept is also extended to the practice of receiver
measurement. An ideal amplifier should add as little noise as possible
to the system, although the laws of quantum mechanics prevent an
amplifier from being entirely noise-free. The total excess noise is
described as the system noise temperature; the definition arises from
the properties of a resistor as a noise generator. Every physical
resistance generates noise, because of thermal fluctuations in the sea
of conduction electrons, and the noise power per unit bandwidth that can
be extracted from the resistor is proportional to its temperature. The
excess noise observed with any radio astronomy receiver can be described
by stating what temperature a resistive load would have to have, when
connected to the input, to generate the observed noise. This turns out
to be an entirely practical way to describe the system, because the
faint continuum radio signals that one deals with are most conveniently
calibrated by using as a reference the continuum noise generated by a
hot (or cold) resistive load.
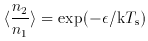
 corresponds to a photon energy h
corresponds to a photon energy h . The
relationship can be inverted, however: for any given average ratio of
populations, there is a corresponding value of the temperature, defined
by Equation (1.1). This defines the state temperature,
Ts.
. The
relationship can be inverted, however: for any given average ratio of
populations, there is a corresponding value of the temperature, defined
by Equation (1.1). This defines the state temperature,
Ts.