There are two main causes for a red UV stellar continuum: 1) ageing of the stellar population; 2) presence of dust (variations of the intrisic IMF will not be discussed here).
An ageing stellar population loses the high-mass, hot stars first, and
then, progressively, lower-mass and colder stars. In the process, the
UV stellar continuum becomes redder and redder and, also, the
4,000 Å break increases in strenght. This break spans a small
wavelength range, thus is unaffected by dust reddening. The strenght
of the 4,000 Å break is therefore a powerful constraint on the age
of the stellar population. The Local starbursts can have very red UV
continua (
> 0),
while still showing rather small 4,000 Å
breaks, telltales of the presence of a young stellar population
( < 107 yr) or of constant star formation (over timescales
~ 109 yr, see
[4]. Ageing of the stellar
population is not the main reason for the presence of a red UV SED in
Local starbursts. Broad-band J, H, and K observations provide limited
information on the strenght of the 4,000 Å break in high-z
galaxies, still accurate enough to exclude ageing as a general cause
for the red UV spectra in this case as well (Dickinson 1997,
priv. communication).
Dust reddening is then the likely cause for red UV spectra, as
demonstrated by the correlation between and color excess
(Figure 1, right panel). Dust reddening
is generally a
close-to-unsolvable problem for unresolved stellar populations (e.g.,
distant galaxies), because the effective obscuration will be a
combination of dust distribution relative to the emitters, scattering,
and environment-dependence of the extinction
([33],
[6]).
The situation gets better in the case of
starbursts because the high energy environment is generally
inhospitable to dust. Shocks from supernovae can destroy dust grains,
while gas outflows can eject significant amounts of interstellar gas
and dust from the site of star formation. If little diffuse dust is
present within the star-forming region, the main source of opacity
will come from the dust surrounding the region. Parametrizing the
``net'' obscuration of the stellar continuum as:
Fobs(
) =
F0()
10-0.4 Es(B-V) k(), with
Fobs() and
F0() the
observed and intrinsic
fluxes, respectively, obscuration in starbursts is expressed as:
The connection between the color excess Es(B - V) and the
measured spectral slope
It is worth stressing that, although dust reddening corrections for
starbursts are parametrized above as a foreground dust screen,
Equation 1 has been derived with NO assumptions on the geometrical
distribution of the dust within the galaxies. Equation 1 is a purely
empirical result ([6],
[4]), which
includes into a single expression any effect of dust geometry, scattering,
and environment-dependence of the dust composition.
Equation 1 provides a recipe for correcting the observed SEDs for the
effects of dust reddening. Does it fully account for the dust
obscuration as well? In other words, does Equation 1 completely
recover the light from the region of star formation or does it misses
the flux from dust-enshrouded regions? The answer to these questions
is a positive one: Equation 1 is able to recover, within a factor
~ 2, the UV-optical light from the entire star-forming region of
UV-bright, i.e. moderately obscured, starbursts.
We can prove the above statement by studying the FIR emission of the
local starbursts. Dust emits in the Far-IR the stellar energy
absorbed in the UV-optical. However, the Far-IR emission is not, by
itself, an unambiguous measure of the opacity of the galaxy, as the
intensity of the dust emission is also a function of the SFR in the
galaxy. A good measure of the total opacity of the galaxy is instead
provided by the ratio FIR/F(UV)
([25]). The Far-IR flux,
FIR, and the UV flux, F(UV), are both proportional to the SFR, but
their sensitivity to dust has opposite trends: roughly, FIR increases
while F(UV) decreases for increasing amounts of dust, although the
details of the trends are dictated by the geometrical distribution of
the dust. In the assumption that the foreground dust screen
parametrization is valid, the FIR/F(UV) ratio is related to the
UV attenuation in magnitudes, A(UV), via
([25]):
where the constant value 1.19 is the combination of the ratio of the
bolometric stellar luminosity to the UV luminosity and the ratio of
the bolometric dust emission to the FIR emission. Since F(UV) and FIR
(e.g., from IRAS) are measurable in galaxies, as is
Figure 2. The attenuation in magnitudes at
1,600 Å, A(1600), as a function of the UV spectral index
How does all this apply to Lyman-break galaxies? The entire purpose of
obtaining dust obscuration corrections for the high-z galaxy sample is
to recover the intrinsic UV emission of the galaxies, therefore
deriving a more meaningful UV luminosity function, a more accurate
value of the SFR for each object (which can bear into the
understanding of the nature of these objects), and, finally, the
intrinsic cosmic SFR density
([22]).
Figure 1 (right
panel) shows the observed UV spectral slopes of the z ~ 3
galaxies. Those slopes can be ``translated'' into a value of the
effective color excess, which is calculated to have mean value
Es(B - V)
Figure 3. The SFR density, in
M
) = 2.656 (-2.310 +
1.315/) + 4.88
1.60 µm
-
0.198/2 +
0.011/3) + 4.88
< 0.63 µm.
is given by the correlation in
Figure 1 (right panel).
, the UV
attenuation can be related to the UV spectral slope via Equation 2
([25]).
Figure 2 shows A(UV) measured at 1,600
Å as
a function of for
a sample of Local starbursts. Overplot on
the data is the trend predicted by Equation 1, with related to
Es(B - V) using Figure
1 and the
limiting case 0 = -2.1 for
Es(B - V) = 0 ([4]). Equation 1 and
Figure 1 have no
adjustable parameters. The agreement between the data and the
predicted trend is therefore impressive, especially if we take into
account that the latter is a recipe for reddening, and could in
principle not account for the entire dust obscuration. Discrepancies
at the low end of the locus of data points in
Figure 2 are
understandable in terms of sample incompletenesses.
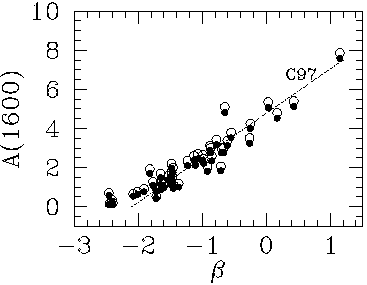
. The data points (empty
and filled circles) are from the same sample of UV-bright, local
starbursts of Figure 1
([18]).
A(1,600) is proportional
to log[FIR/F(UV)] where FIR and F(UV) are the Far-IR and UV
observed luminosities, respectively (see text). The filled and empty circles
correspond to two different choices of the bolometric-to-FIR
correction for the dust emission. This is the most uncertain parameter
in the derivation of Equation 2; yet, its effect on the data is fairly
small. The straight line across the data, marked C97, is the location
of the reddening curve of Equation 1, with 0 = -2.1 for
Es(B - V) = 0
([4]).
There are no adjustable parameters in
the positioning of the C97 line. The agreement between the data
points and the predicted attenuations from the reddening curve (Equation 1)
demonstrates that reddening corrections can fully recover the intrinsic
UV emission from these galaxies and the amount of star formation buried
in dust is relatively small.
0.15 for the z ~ 3 galaxies, or an attenuation
A(1600) 1.6 mag
([31], see also
[3]).
Incidentally, this mean value of
Es(B - V) is
similar to that observed in the local starburst sample
([3]);
this is purely coincidental, and is borne of the
fact that the two samples of galaxies cover similar ranges of
. A similar mean
value of the effective color excess has been
obtained by Pettini et al.
([27]) from the
analysis of
the nebular emission lines in the NIR spectra of a small sample of
Lyman-break galaxies. Correcting the observed UV spectra for dust
attenuation increases the median SFR of 
x5 in the z > 2
galaxies and of x3 in the
z 1 galaxies
(Figure 3). The difference in the correction
factors at low and high-z
is entirely due to the different wavelengths at which the two redshift
regimes are probed: ~ 1,600 Å the high-z galaxies and
~ 2,800 Å the lower-z galaxies. The dust correction factors
have been ``measured'' only for the high-z sample and have been assumed
to hold unchanged for the z
1 sample, modulo the change in wavelength (see discussion in
[31]).
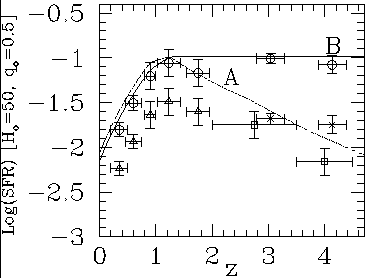
yr-1 Mpc-3,
as a function of redshift z. The data points are derived from the UV
luminosity density of galaxies, converted to SFR using a Salpeter IMF
in the range 0.35-100 M and continuous SF. The triangles
are the observed values at 2,800 Å of Lilly et
al. ([20])
and Connolly et
al. ([7]).
The squares are the observed values
at ~ 1,600 Å as reported in Madau et al.
([23]),
while the crosses are the new values from the Lyman-break galaxies by
Steidel et al.
([31]).
The circles represent the
intrinsic SFR densities from the data of Lilly et al., Connolly et
al., and Steidel et al., corrected for dust obscuration using
Es(B - V) = 0.15 (see
[31]).
The curves marked A and
B bracket the range of solutions for the intrinsic SFR density
from the evolution model described in
Section 4. Curve B agrees well
with the obscuration-corrected data points (circles).