| © CAMBRIDGE UNIVERSITY PRESS 1997
| |
1.3 Properties of Quasars
By late 1964, Schmidt had studied a sufficient number of quasars to define their properties (Schmidt 1969):
Not all objects that we now call AGNs share every one of these properties. In fact, the single most common characteristic of AGNs is probably that they are all luminous X-ray sources (Elvis et al. 1978). Nevertheless, the characteristics identified by Schmidt are important for understanding the physics of AGNs and as well as understanding the techniques by which AGNs are found. We will therefore discuss these various properties individually below.
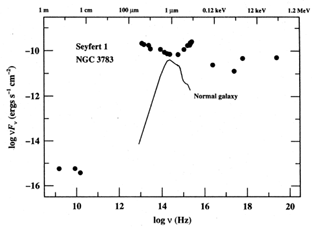
In more modern terms, one of the defining characteristics of quasars is their very broad spectral energy distribution, or SED (Fig. 1.3). Quasars are among the most luminous objects in the sky at every wavelength at which they have been observed. Unlike spectra of stars or galaxies, AGN spectra cannot be described in terms of blackbody emission at a single temperature, or as a composite over a small range in temperature. Non-thermal processes, primarily incoherent synchrotron radiation, were thus invoked early on to explain quasar spectra.
|
Figure 1.3. The spectral energy distribution
(SED) of the Seyfert 1 galaxy NGC 3783
(Alloin et al. 1995)
from radio to |
In general, the broad-band SED of a quasar continuum can be characterized crudely as a power law
where
so an equivalent form to eq. (1.5) is F
Fits to quasar spectra over large frequency ranges yield spectral
indices that are typically in the range 0
The case
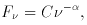
is the power-law index,
C is a constant, and F
is the
specific flux (i.e., per unit frequency interval), usually measured in
units of ergs s-1 cm-2 Hz-1. The
convention that we adopt throughout
this book is that a positive spectral index characterizes a source
whose flux density decreases with increasing frequency. The reader is
cautioned that some authors absorb the minus sign into the definition
of the spectral index (e.g., F = C). Specific fluxes, particularly
in the ultraviolet and optical parts of the spectrum, are often
measured per unit wavelength interval (i.e., in units of ergs
s-1 cm-2 Å-1) rather than per unit
frequency interval. The total flux measured
in any bandpass is the same, of course, whether the bandwidth is
measured in frequency or in wavelength, so the relationship F d = F
d
always holds. The transformation between the two systems is thus
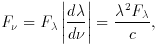
= C' -2.
1, but different values of
are found for different
spectral ranges. Indeed, it is obvious that
a single power law cannot hold over all frequencies as the integrated
power would diverge either at high frequencies (for 
1) or at low
frequencies (for 
1). Over a frequency range 1 - 2, the total power received is
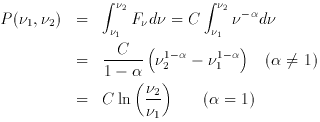
= 0, a ``flat
spectrum'' on a conventional plot of specific
flux versus frequency, has equal energy per unit frequency interval
and the case = 1 has equal
energy per unit logarithmic frequency
interval 1.
A useful way to plot the broad-band SED in quasars is on a
log F versus log diagram, as in
Fig. 1.3. In this case, the
power-law distribution becomes
F 
1-, so the
case = 1 is a
horizontal line in such a diagram, and the = 0 spectrum rises with
frequency. This is the preferred format for examining where the quasar
energy is actually emitted as it reflects the amount of energy emitted
in each equally spaced interval on the logarithmic frequency axis.
1 The case = 1 is sometimes described as having equal energy per
decade (or octave), i.e., over any factor of 10 (or two) in frequency.
Back.
-ray
energies. Shown for comparison is SED for a normal (type Sbc) galaxy,
from a template spectrum compiled by