Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
499-542 Copyright © 1992 by Annual Reviews. All rights reserved |
5.1 Wormholes and the Cosmological Constant
One of the most provocative explanations for the small value of the cosmological constant invokes quantum cosmology and fluctuations in the topology of spacetime known as ``wormholes.'' Although we will not give a technical description of the relevant arguments, we will try to give a pedagogical introduction to the essential ideas and the troubles with their realization.
Quantum cosmology is the study of the universe as a quantum
gravitational system
(Wheeler 1968,
DeWitt 1967).
Since one does not
have a consistent quantum theory of gravity, it is common to use
approximation schemes based on Feynman's path integral formulation of
quantum mechanics
(Feynman & Hibbs
1965).
In this picture, we compute
the wavefunction for a particle with initial state
 0 to be in state
0 to be in state
 by integrating over all paths that connect the two states:
by integrating over all paths that connect the two states:
where p is a path from
Since an oscillating integral such as that of Equation 35 will
generally not converge, it is common to analytically continue the time
parameter to imaginary values: t ->
i
where M is a four-dimensional Euclidean space containing a three
dimensional slice
Observation tells us that our universe is large and smooth on a
global scale; therefore, our next step is to estimate the integral in
Equation 36 for three-surfaces
where g is the determinant of the metric
gµv and R is the Ricci scalar
(R
Since Equation 37 is simply the action for general relativity, its
stationary point is the solution to Einstein's equations with
cosmological constant; in Euclidean space, this is a four-dimensional
sphere. For such spaces, R =
4
If we consider
However, the cosmological constant may not normally be thought of as
a free parameter. Hawking
(1984;
see also
Baum 1984)
proposed a field
which would contribute to the action in such a way as to mimic a
cosmological constant; this field would be varied in the path
integral, turning
A more natural mechanism for making
Figure 11. Example of a Euclidean space
that contributes to the Feynman
path integral for quantum cosmology. This manifold consists of large
spheres connected by wormholes.
This is essentially the argument assembled by Coleman in his
celebrated paper
(Coleman 1988b).
(See also
Banks 1988:
for later variations, see
Accetta et al 1989,
Adler 1989,
Elizalde &
Gaztanaga 1990,
Hosoya 1989,
Kosower 1989,
Rubakov 1988,
Unruh 1989b, and
Veneziano 1989.)
One subtlety arises because there are many connected
spheres contributing to the path integral; the associated
combinatorics makes the wave function of the universe a double
exponential,
At the same time, there are many unanswered questions relating to
Coleman's proposal; we will mention just a few. Before looking at
worm-holes specifically, it is worth noting a long-standing problem of
quantum cosmology: The Euclidean action for gravitation is not bounded
below, and therefore the path integral of Equation 36 does not
converge. Many remedies to this problem have been proposed, including
allowing to vary along a complex contour
(Gibbons et al 1978),
adding
additional terms to the action such that it becomes bounded below
(Horowitz 1985),
or staying in Lorentzian-signature space all along
(Farhi 1989,
Strominger 1989).
Unfortunately, the solution to the cosmological constant problem seems
to depend intimately on the ``wrong'' sign for the action
(Giddings &
Strominger 1989),
and attempts to base analogous calculations in
Lorentzian space do not find a peak at
If we accept for the moment the viability of Euclidean quantum
gravity, there is still some question of the reliability of
approximating the path integral by large spheres connected by small
wormholes. V. Kaplunovsky (unpublished) and
Fischler & Susskind
(1989)
have suggested that large wormholes may dominate small ones; since
then a debate has raged back and forth with no clear winner
(Preskill 1989;
Coleman & Lee 1989,
1990;
Polchinski 1989a;
Iwazaki 1989).
Equally troubling is an argument by
Polchinski (1989b)
that the integration over spheres connected by worm-holes induces a phase
(-i)d + 2 in the wave function, where d is
the dimension of spacetime. Thus, in a four-dimensional universe
These results serve to emphasize that quantum cosmology is an
ambitious but unsettled subject, insufficiently developed for crucial
questions to be definitively answered. The solution to the
cosmological constant problem offered by wormholes is certainly
elegant as well as provocative; only further work will allow us to
judge its physical relevance.
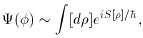
 0
to
0
to  , and
S[
, and
S[ ] is the
action for the
path. In quantum cosmology, a ``state'' is a three-dimensional slice
] is the
action for the
path. In quantum cosmology, a ``state'' is a three-dimensional slice
 of a four-dimensional spacetime, and the wave function of a particle
is replaced by the ``wave function of the universe''
of a four-dimensional spacetime, and the wave function of a particle
is replaced by the ``wave function of the universe''
 (
( ), which is the probability amplitude that the universe contains
), which is the probability amplitude that the universe contains
 .
.
 . This transformation changes the
signature of the metric from (- + + +) to (+ + + +), so the resulting
paths are in a Euclidean space rather than a Lorentzian one. At the
same time, the action becomes imaginary, so that we may write S
-> i SE,
where SE is called the Euclidean action. The path
integral is then
damped by a decaying exponential, and will converge if
SE is bounded
below. In quantum cosmology, this transformation implies that we
should integrate over manifolds of Euclidean signature rather than
Lorentzian spacetimes. We therefore compute the wave function of the
universe via
. This transformation changes the
signature of the metric from (- + + +) to (+ + + +), so the resulting
paths are in a Euclidean space rather than a Lorentzian one. At the
same time, the action becomes imaginary, so that we may write S
-> i SE,
where SE is called the Euclidean action. The path
integral is then
damped by a decaying exponential, and will converge if
SE is bounded
below. In quantum cosmology, this transformation implies that we
should integrate over manifolds of Euclidean signature rather than
Lorentzian spacetimes. We therefore compute the wave function of the
universe via
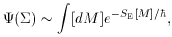
 . (We will not
discuss the contentious issue of boundary conditions; see
Hartle & Hawking 1983;
Vilenkin 1982,
1988;
Linde 1984).
. (We will not
discuss the contentious issue of boundary conditions; see
Hartle & Hawking 1983;
Vilenkin 1982,
1988;
Linde 1984).
 which are large and smooth. Although
performing the integral is well beyond our capabilities, it is
possible to estimate it as the exponential of an ``effective action''
which are large and smooth. Although
performing the integral is well beyond our capabilities, it is
possible to estimate it as the exponential of an ``effective action''
 [M]. The effective
action may be thought of as an action with all
quantum fluctuations integrated out:
[M]. The effective
action may be thought of as an action with all
quantum fluctuations integrated out:
 [dM] exp (-
SE[M] /
[dM] exp (-
SE[M] /  ) = exp (-
) = exp (- [Mc] /
[Mc] /  ), where Mc is the ``classical'' space, for
which
), where Mc is the ``classical'' space, for
which  is stationary. As
Coleman (1988b)
points out, it may not seem very useful
to define a function (
is stationary. As
Coleman (1988b)
points out, it may not seem very useful
to define a function ( ) in
terms of a path integral over another
function (SE) which we do not know; however, an
approximate expression
for
) in
terms of a path integral over another
function (SE) which we do not know; however, an
approximate expression
for  for large spaces is
known. The leading terms are simply those of
the (Euclidean) action for general relativity:
for large spaces is
known. The leading terms are simply those of
the (Euclidean) action for general relativity:
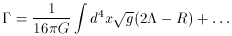
 gµv Rµv). This expression
may be roughly thought of as a power series
expansion in the inverse size of the space; for large manifolds,
gravitation is always dominant, and we may neglect terms representing
other fields.
gµv Rµv). This expression
may be roughly thought of as a power series
expansion in the inverse size of the space; for large manifolds,
gravitation is always dominant, and we may neglect terms representing
other fields.
 and
and
 d4 x
d4 x  g = 24
g = 24 2
/
2
/  2. Inserting these
into Equation 37 yields
2. Inserting these
into Equation 37 yields  = -
3
= -
3 / G
/ G . Since the path integral in
Equation 36 is the exponential of
-
. Since the path integral in
Equation 36 is the exponential of
- /
/  , we have
, we have
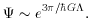
 as an
independent parameter, this expression is
infinitely peaked at
as an
independent parameter, this expression is
infinitely peaked at  = 0:
the cosmological constant problem is
solved! The answer is simply that universes in which
= 0:
the cosmological constant problem is
solved! The answer is simply that universes in which
 = 0 dominate
the path integral, making it overwhelmingly probable that the
cosmological constant vanishes.
= 0 dominate
the path integral, making it overwhelmingly probable that the
cosmological constant vanishes.
 into a
free parameter and making Equation 38 the
wave function of the universe. However, there is no compelling reason
to believe in the existence of such a field (except for solving the
cosmological constant problem).
into a
free parameter and making Equation 38 the
wave function of the universe. However, there is no compelling reason
to believe in the existence of such a field (except for solving the
cosmological constant problem).
 a free parameter is provided
by wormholes - topologically nontrivial spacetime geometries. Roughly,
a wormhole may be thought of as a thin tube which connects two
separated regions of a Euclidean space (see
Figure 11). (The Euclidean
wormholes we consider are distinct from wormholes which connect
spatial regions in a Lorentzian geometry; see
Wheeler 1964 and
Morris et al 1988.)
Since the action for an infinitesimally small wormhole is
negligible, manifolds consisting of large spheres connected by
wormholes are approximate stationary points of the effective action
(Equation 37), and therefore contribute to the path integral; the
effect of these configurations has been the object of some debate
(Hawking 1979,
1982,
1988;
Teitelboim 1982;
Strominger 1984;
Gross 1984;
Lavrelashvili et al
1987).
A resolution was provided by
Coleman (1988a) and
Giddings &
Strominger (1988),
who found that wormholes
induced a distribution of values for all the constants of
nature-precisely what is necessary to solve the cosmological constant
problem. In other words, the interaction of our ``universe'' with other
universes through wormholes allows the cosmological constant to attain
a range of values; since the effective action is stationary at
a free parameter is provided
by wormholes - topologically nontrivial spacetime geometries. Roughly,
a wormhole may be thought of as a thin tube which connects two
separated regions of a Euclidean space (see
Figure 11). (The Euclidean
wormholes we consider are distinct from wormholes which connect
spatial regions in a Lorentzian geometry; see
Wheeler 1964 and
Morris et al 1988.)
Since the action for an infinitesimally small wormhole is
negligible, manifolds consisting of large spheres connected by
wormholes are approximate stationary points of the effective action
(Equation 37), and therefore contribute to the path integral; the
effect of these configurations has been the object of some debate
(Hawking 1979,
1982,
1988;
Teitelboim 1982;
Strominger 1984;
Gross 1984;
Lavrelashvili et al
1987).
A resolution was provided by
Coleman (1988a) and
Giddings &
Strominger (1988),
who found that wormholes
induced a distribution of values for all the constants of
nature-precisely what is necessary to solve the cosmological constant
problem. In other words, the interaction of our ``universe'' with other
universes through wormholes allows the cosmological constant to attain
a range of values; since the effective action is stationary at
 = 0,
this value is singled out. (One must not take this concept too
literally - the universes being spoken of are fictional Euclidean
spaces used to calculate a path integral, not alternate worlds that
coexist with our own.)
= 0,
this value is singled out. (One must not take this concept too
literally - the universes being spoken of are fictional Euclidean
spaces used to calculate a path integral, not alternate worlds that
coexist with our own.)
 ~ exp
(e3
~ exp
(e3 /
/  G
G ) this displays the infinite peak at
) this displays the infinite peak at
 = 0
in an even more impressive way. As a solution to the cosmological
constant problem, this proposal has at least two very favorable
features. First, although highly speculative physics is essential to
the argument, there was no need to introduce any new laws or invent
new phenomena; all that was necessary was to include in the path
integral wormhole configurations which should be there anyway. Second,
the communication with other large universes explains how our universe
``knows ahead of time'' to set
= 0
in an even more impressive way. As a solution to the cosmological
constant problem, this proposal has at least two very favorable
features. First, although highly speculative physics is essential to
the argument, there was no need to introduce any new laws or invent
new phenomena; all that was necessary was to include in the path
integral wormhole configurations which should be there anyway. Second,
the communication with other large universes explains how our universe
``knows ahead of time'' to set
 = 0 at low temperature,
rather than at
early times. In Coleman's phrase, ``prearrangement is replaced by
precognition''
(Coleman 1988b).
= 0 at low temperature,
rather than at
early times. In Coleman's phrase, ``prearrangement is replaced by
precognition''
(Coleman 1988b).
 = 0
(Fischler et al 1989,
Cline 1989).
= 0
(Fischler et al 1989,
Cline 1989).
 ~ exp (-e3
~ exp (-e3 /
/  G
G ), which
exhibits no peak at
), which
exhibits no peak at  =
0. Lastly, several authors have explored a suggestion by
Coleman (1988b)
that wormholes may determine all of the
constants of nature. To date, attempts to implement this plan have not
met with great success
(Preskill 1989,
Hawking 1990,
Klebanov et al 1989,
Preskill et al 1989).
=
0. Lastly, several authors have explored a suggestion by
Coleman (1988b)
that wormholes may determine all of the
constants of nature. To date, attempts to implement this plan have not
met with great success
(Preskill 1989,
Hawking 1990,
Klebanov et al 1989,
Preskill et al 1989).