In Madore & Freedman (1991) we published fiducial PL relations in seven bandpasses: BVRIJHK. These were all based on selecting self-consistent sets of previously published LMC Cepheid data, scaled to an LMC true distance modulus of 18.50 mag and applying a single line-of-sight reddening correction using E (B-V) = 0.10 mag. Thirty-two stars were available for a calibration of BVRI PL relations; 25 stars were used for an alternative set of BVRIJHK calibrations. In the following we compare those multiwavelength PL relations with the Hipparcos sample of Galactic Cepheids, individually corrected for foreground reddening and scaled to their geometric parallax distances. We have collected from the literature multiwavelength (BVIJHK) mean magnitudes for as many of the Hipparcos-calibrating Cepheids as have been published (notably for the infrared Wisniewski & Johnson 1968, Welch et al. 1984, Laney & Stobie 1992 and reference therein). These form rather disjoint subsets. After eliminating the suspected overtone pulsators listed by FC97, the total available sample with parallaxes drops from 26 to 20. Of these only 7 have mean magnitudes published at all six wavelengths, while 10 and 13 Cepheids, respectively have either BVIJK or BVJK magnitudes in common. We have analyzed these four groups of stars independently, but self-consistently, in the following way.
Using the Hipparcos parallaxes and Galactic reddenings adopted by FC97 from Fernie, Kamper & Seager (1993) scaled to the various wavelengths using the extinction law of Cardelli et al. (1989), we derived absolute magnitudes for each of the Cepheids in each of the observed wavelengths. (We note that these corrections for interstellar extinction are not inconsiderable, ranging up to 2 mag in B for several stars). The resulting PL relations are shown in the six panels of Figure 27. Error bars are one-sigma uncertainties from the quoted parallaxes. Note the highly correlated nature of the individual data points about the fiducial lines. And too, we remind the reader that the computation of distances and their related errors from observed parallaxes is non-trivial (Brown et al. 1997), as distances are not linearly related to parallaxes, and parallax errors can subtly bias samples. A full treatment of this issue is beyond the scope of this paper, but we note that selection biases at least are minimized for stars having the smallest reported errors. As discussed by Brown et al., given the true parallax distribution the expected biases follow naturally; however, corrections to the observed parallaxes require assumptions about the true distribution, and detailed modeling. Fortunately for this application the Cepheid sample is not parallax-selected; the objects being chosen in advance based on their optical variability, periods and apparent magnitudes.
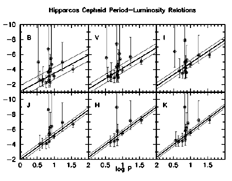Figure 27. Multiwavelength
Period-Luminosity relations for Cepheids with Hipparcos parallaxes,
plotting all stars that have data available at the particular
wavelength, as noted in the upper left corner of each panel. In each
panel the solid sloping line is not a fit to the data, but rather it is
the published calibration of
Madore & Freedman (1991)
flanked by thin
parallel lines representing the 2-
limits quoted by them as being the intrinsic width of
the instability strip at each wavelength.
The differences between these individual (trigonometric) absolute magnitudes and the predicted BVIJHK magnitudes derived from the mean PL relations of MF91 (solid lines in Figure 27) are each plotted in Figure 28 against the corresponding B-band residual. The (B-V) intrinsic color residuals are plotted against the B-band residuals in the upper right panel. The individual residuals at a given wavelength contain random contributions from the parallax uncertainties, reddening errors, and finally the intrinsic (temperature-induced) magnitude residuals which reflect the finite width of the Cepheid instability strip. The observed residuals are however extremely large (nearly 5 mag peak-to-peak) and are almost certainly dominated by the (achromatic) errors in the parallaxes, given the strict unit-slope correlation of the mag-mag residuals, and the total lack of any correlation between the magnitude-color residuals (Figure 28).
Figure 28. B-band residuals from the
multiwavelength Period-Luminosity relations in
Figure 27 are
sequentially plotted as a function of residuals from each of the other
five PL relations and (upper right panel) against the (B-V) color
residuals. The total lack of correlation in the latter instance is
unexpected except in the limit where the residuals are dominated by
distance errors in the derived parallaxes. This latter situation is
apparently the case given the strong (unit-slope) correlations of the
residuals in each of the other panels, regardless of wavelength.
Wavelength-dependent offsets between the six mean solutions independently will reflect (1) errors in the adopted true distance to the LMC (which set all of the zero points in the MF91 multiwavelength PL relation calibrations), (2) reddening errors in the adopted extinction to the LMC sample of calibrating Cepheids, and finally (3) intrinsic differences between the LMC and Galactic Cepheids, for example, due to metallicity.
Our first solution considers the largest data set (in terms of
parallaxes) but the one that is most restricted in terms of wavelength
coverage: it consists of 19 Cepheids observed in B and V.
Weighted by the square of the signal-to-noise ratio in the Hipparcos
parallax, the residuals were summed and averaged at each of the two
wavelengths giving mean offsets between the LMC calibration and the
Galactic Cepheids. The variance in each mean offset was then
calculated from the average of the squares of these same residuals
again inversely weighted by the variance in the individually quoted
parallaxes. The differences are 
B = +0.23 ± 0.35 mag and
V = +0.16 ±
0.28 mag, in the sense that the LMC Cepheid
calibration appears to be too faint with respect to the Galactic
calibration. (Further restricting the sample to only those 12 stars
with 
/ > 2.0 changes B to +0.22 ± 0.24
mag and
V
If the (statistically marginal, but apparently systematic) differences
in the B and V solutions were to be ascribed to reddening alone,
then the Galactic data and the LMC calibration can be reconciled by
invoking an increase of E (B-V) = 0.07 mag in the adopted mean
reddening to the LMC Cepheid sample. This is consistent with a
similar
suggestion regarding the LMC Cepheid calibration made recently by
Bohm-Vitense (1997)
based on different data. This reddening solution
has the consequence that it would also require the distance modulus of
the LMC to be revised downwards by -0.06 mag to
18.44 mag; the
uncertainty on this offset being at least as large as the uncertainty
in the individual moduli (± 0.3 mag), depending on the degree of
correlation in those cumulative uncertainties. This particular path,
of a reddening solution, cannot be considered definitive. Other
possibilities are: (1) the LMC true modulus should be increased by
(0.23 + 0.16) / 2 = +0.20 mag, without any change to the foreground
reddening, or (2) that there are differential metallicity corrections
amounting to -0.23 and -0.16 mag that need to be applied at the
B and V wavelengths, respectively. Of course, any suitably
contrived linear combination of the above three effects could also be
invoked. More constraints on the problem are obviously needed.
An alternative possibility is that some of the wavelength-dependent
effects seen in the comparison of Galactic (high metallicity) data
with the LMC (lower metallicity) data could be due to
chemical composition differences between the two samples. Taken at face value
the dependence of the apparent V modulus on metallicity would be
very large, V /
[Fe / H] =
0.16 / 0.15 = 1.1 (± 1.9) mag/dex, assuming that the full offset in
V noted in the above comparison is due to metallicity, and
adopting a metallicity underabundance of 1.4x between the LMC and the
Solar neighborhood (see, for example,
FW87).
However, we note that this
effect is basically indistinguishable from reddening in its form (as
evidenced by our first set of solutions), and that the offset
(whatever its origin) when treated as reddening leads to a true
distance modulus for the LMC that is unchanged, from previous
assumptions, at 18.50 mag. Given this apparent degeneracy between
reddening and metallicity, and the current large uncertainties in the
parallaxes, assessing the dependence on metallicity from these data
alone will remain problematic.
To obtain added leverage on the solution, moving to the infrared has numerous well known advantages, as first articulated in McGonegal et al. (1982): reddening effects are known to decrease with wavelength, in a well defined and calibrated manner; and simultaneously, metallicity effects are also expected to decrease in amplitude with increased wavelength.
Our second solution is based on 13 Cepheids each having BVJK data in
common. This four-color solution gives a derived reddening
increase for the LMC Cepheid sample of +0.04 ± 0.08 mag, with no
formal offset in the derived 18.50 ± 0.13 mag true modulus for the
LMC. Our next approximation employs 10 Cepheids each
now having
BVIJK mean magnitudes. Here the formal solution for the true modulus
for the LMC is 18.53 ± 0.14 mag, with a corresponding
increase in
the mean reddening of +0.06 ± 0.07 mag. Finally, we have analyzed
a sample of 7 Galactic Cepheids, each having BVIJHK photometry, to
obtain one last solution: E (B-V) = 0.07 ± 0.07 mag with
(m-M) LMC = 18.57 ± 0.11 mag. The fit to
this
final set of observations is shown in Figure
29; the 
2 weighted residual
fitting surface being shown as an inset. The individual apparent
moduli discussed here, and their errors, are summarized in Table 1.
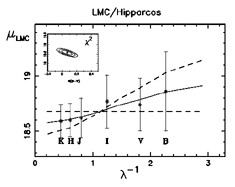Figure 29. Apparent modulus plots for
LMC Cepheids observed at BVIJHK scaled to the
Hipparcos zero
point and using the published multiwavelength PL solutions of
Madore & Freedman (1991).
The solid line is a weighted 2 fit of a reddening
line to the data; the broken line indicates the one-sigma limits on that
solution. Inset (top left) shows the 2 surface indicating the minimization solution for
the modulus and reddening and the interdependence of their associated
errors.
| No.Stars | µB ±
| µV ±
| µI ±
| µJ ±
| µH ±
| µK ±
|
|---|---|---|---|---|---|---|
| 19 | 18.73 ± 0.35 | 18.66 ± 0.28 | . . . | . . . | . . . | . . . |
| 13 | 18.71 ± 0.36 | 18.64 ± 0.24 | . . . | 18.44 ± 0.23 | . . . | 18.54 ± 0.13 |
| 10 | 18.74 ± 0.36 | 18.67 ± 0.24 | 18.71 ± 0.20 | 18.44 ± 0.24 | . . . | 18.57 ± 0.14 |
| 7 | 18.86 ± 0.36 | 18.74 ± 0.24 | 18.77 ± 0.24 | 18.62 ± 0.18 | 18.60 ± 0.15 | 18.59 ± 0.15 |
Finally, if we now adopt the metallicity correction of V = 0.04 mag advocated
by FC97
and assume that the effects at JHK are negligible, (and
eliminate B and I from the solution given that
metallicity corrections for these filters are not well defined at this
time) we find for this 4-color solution E (B-V) = 0.06 ±
0.11 mag with (m-M) LMC = 18.57 ± 0.11 mag. This is
virtually indistinguishable from the full BVIJHK solution given
above.