


The basic physics connecting the luminosity and color of a Cepheid to its period is well understood. Using Stephan's law
the bolometric luminosities L of all stars,
(including Cepheids), can be derived. The radius R is a
geometric term, parameterizing the total emitting surface area 4
and it is schematically shown in Figure 2. It
should be
noted that the entire MBOL - log
Te plane is mapped by Equation (2), and that
within the context of this
relation alone, for any value of log Te, an unbounded range
of radius R is independently possible. However, once R
and Te are each specified,
MBOL is uniquely
defined. Additional constraints, outside of Stephan's Law itself, must
be involved if bounds on permitted values of the independent geometric
and thermal variables are to be considered. An important constraint is
provided by stellar evolution. In terms of timescales and allowed
equilibrium configurations, the core-hydrogen-burning main sequence is
one of the most striking and well known examples of such a
``constraint'' on populating the HR diagram. Hydrostatic
equilibrium can be achieved for long periods of time along the
hydrogen-burning main sequence, and as a result we are constrained to
observe most of the stars there most of the time. There are, of course,
other constraints.
For mechanical systems it is well known that P
If we then linearly map log (Te) into an observable
intrinsic color (i.e., B-V), and map radius into an
observable period, we thereby predict a new two-parameter description
of the luminosity of (pulsating) stars. This is precisely the physical
basis for the period-luminosity-color (PLC) relation for Cepheids, as
was so elegantly introduced and explained over a quarter of a century
ago
(Sandage 1958,
Sandage & Gratton 1963,
Sandage & Tammann 1968).
In its linearized form for pulsating variables, Stefan's law takes on
the following form of the PLC: MV =
Stars can be found evolving across many parts of the color-magnitude
diagram. However, only in very narrowly defined regions do they become
pulsationally unstable. Cepheid pulsation in particular occurs because
of the changing atmospheric opacity with temperature in the helium
ionization zone. This zone acts like a heat engine and valve
mechanism, alternately trapping and then releasing energy, thereby
periodically forcing the outer layers of the star into motion against
the restoring force of gravity. Not all stars are unstable to this
mechanism. The cool (red) edge of the Cepheid instability strip is
thought to be controlled by the onset of convection, which then
prevents the helium ionization zone from driving the pulsation (see
Baker & Kippenhahn 1965;
and Deupree 1977
for references). For hotter
temperatures a blue edge is encountered when the helium ionization
zone is found too far out in the atmosphere for significant pulsations
to occur. Further details and extensive references can be found in the
monograph on stellar pulsation by
Cox (1980).
 R2
R2  Te4
Te4
 R2, and the
effective temperature Te is a thermal term, used to
parameterize the areal surface brightness, given by
R2, and the
effective temperature Te is a thermal term, used to
parameterize the areal surface brightness, given by
 Te4. Expressed in magnitudes, Stephan's
Law becomes
Te4. Expressed in magnitudes, Stephan's
Law becomes
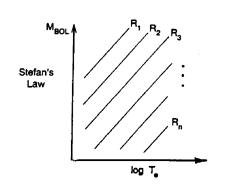 Figure 2. Stefan's Law expressed in
graphical form projected onto the theoretical MBOL -
logTe plane where loci of constant radius are
indicated by upward sloping lines.
Figure 2. Stefan's Law expressed in
graphical form projected onto the theoretical MBOL -
logTe plane where loci of constant radius are
indicated by upward sloping lines.
 1/2 =
Q , where
Q is a structural constant, and P is the natural
free pulsation period, determined by gravity through
1/2 =
Q , where
Q is a structural constant, and P is the natural
free pulsation period, determined by gravity through  , the mean
density of the system, in turn defined by M = 4/3
, the mean
density of the system, in turn defined by M = 4/3  R3
R3  , where M
is the total mass
of the system. If it is assumed that mass is predominantly a function
of R and Teff, then the pulsation period
can be used as the second observable parameter instead of
requiring the radius to be observed directly.
, where M
is the total mass
of the system. If it is assumed that mass is predominantly a function
of R and Teff, then the pulsation period
can be used as the second observable parameter instead of
requiring the radius to be observed directly.
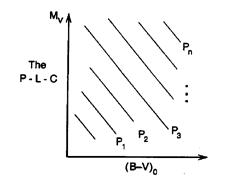 Figure 3. The PLC relation expressed in
graphical form as projected onto the observational MV
- (B-V) plane, where loci of constant period are downward sloping
lines.
Figure 3. The PLC relation expressed in
graphical form as projected onto the observational MV
- (B-V) plane, where loci of constant period are downward sloping
lines.
 logP +
logP +  (B-V) 0 +
(B-V) 0 +  . In analogy to plotting Stephan's Law in
the theoretical MBOL - log Te
above, Figure 4 shows the PLC mapped into the
observational M0 - (B-V) 0
color-magnitude diagram. Again the entire plane is mapped. To see how
the PLC relates to the more commonly referred to relations (the PL and
PC relations), the reader is referred to a more detailed discussion in
the sections ahead, the caption to Figure 4,
and the Cepheid section in
Jacoby et al. (1992)
where an empirical analog of Figure 4 is given.
. In analogy to plotting Stephan's Law in
the theoretical MBOL - log Te
above, Figure 4 shows the PLC mapped into the
observational M0 - (B-V) 0
color-magnitude diagram. Again the entire plane is mapped. To see how
the PLC relates to the more commonly referred to relations (the PL and
PC relations), the reader is referred to a more detailed discussion in
the sections ahead, the caption to Figure 4,
and the Cepheid section in
Jacoby et al. (1992)
where an empirical analog of Figure 4 is given.
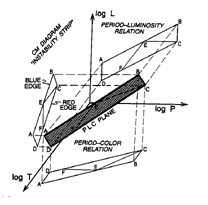 Figure 4. The Cepheid Manifold:
Projections of the PLC plane (shown shaded) onto the three principal
co-ordinate systems (luminosity [L], increasing up, period [log P],
increasing to the right and color [(B-V)] becoming bluer to the lower
left). The backward projection onto the L-P plane gives the period-luminosity
relation. Projecting to the left gives the position of instability
strip within the color-magnitude diagram. Projecting down gives the
period-color relation.
Figure 4. The Cepheid Manifold:
Projections of the PLC plane (shown shaded) onto the three principal
co-ordinate systems (luminosity [L], increasing up, period [log P],
increasing to the right and color [(B-V)] becoming bluer to the lower
left). The backward projection onto the L-P plane gives the period-luminosity
relation. Projecting to the left gives the position of instability
strip within the color-magnitude diagram. Projecting down gives the
period-color relation.
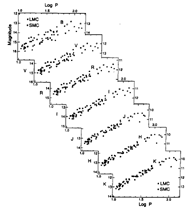 Figure 5. Magellanic Cloud Cepheid
period-luminosity relations at seven wavelengths, from the blue to the
infrared, constructed from a self-consistent data set
(Madore & Freedman 1991).
LMC Cepheids are shown as filled circles; SMC data, shifted to the LMC
modulus, are shown as open circles. Note the decreased width and the
increased slope of the relations as longer and longer wavelengths are
considered.
Figure 5. Magellanic Cloud Cepheid
period-luminosity relations at seven wavelengths, from the blue to the
infrared, constructed from a self-consistent data set
(Madore & Freedman 1991).
LMC Cepheids are shown as filled circles; SMC data, shifted to the LMC
modulus, are shown as open circles. Note the decreased width and the
increased slope of the relations as longer and longer wavelengths are
considered.