


3.2 Density Inhomogeneities in the Early Universe
The density fluctuations inferred from COBE are remarkably small and we know
that for the overdensities in our own galaxy 
 /
/  > 1;
furthermore, gravitationally collapsed structures, such as quasi stellar
objects, are known
to exist at z
> 1;
furthermore, gravitationally collapsed structures, such as quasi stellar
objects, are known
to exist at z  5, so by
this time at least some
perturbations must have grown past
5, so by
this time at least some
perturbations must have grown past 
 /
/  = 1. The big questions
for galaxy formation then are: What is the scale-size of the first
collapsing overdensities? How fast can fluctuations grow in the early
Universe? What sort of fluctuations must they be?
= 1. The big questions
for galaxy formation then are: What is the scale-size of the first
collapsing overdensities? How fast can fluctuations grow in the early
Universe? What sort of fluctuations must they be?
In 1902 James Jeans considered the criterion for gravitational collapse in
an infinite uniform medium in which small density perturbations
(d )
give rise to adiabatic pressure changes or acoustic waves (dp), such
that
)
give rise to adiabatic pressure changes or acoustic waves (dp), such
that
where V2s is the adiabatic sound speed. The
criterion for
collapse is satisfied by a mass (known as the Jeans Mass, MJ)
just large enough
that the sound crossing time is larger than the free-fall collapse time
- thus rendering the overdensity unable to respond with pressure changes
fast enough to halt
gravitational collapse.
It is straight forward to apply the basic idea of
Jeans to the problem of galaxy formation in the early Universe and
calculate the minimum spherical mass which would stop expanding with the
universal Hubble flow, turn around, and gravitationally collapse. At
z = 1000, just after decoupling
where
This value assumes that
the energy density of the Universe is matter dominated - at epochs earlier
than about the decoupling stage (z >1000 or t
This mass is so large that it is in fact comparable to the entire baryonic
content of each causally connected volume of space at any time during the
radiation
dominated era. Furthermore, the characteristic timescale required for
matter fluctuations to collapse is longer than
the characteristic time for the expansion of the Universe during this era.
A combination of the large Jeans mass and rapid expansion
time of the Universe guarantee that no baryonic fluctuations
gravitationally
collapse for the first 106 yrs after the Big Bang and galaxy
formation really only begins after this time at the onset of the matter
dominated era.
An estimate of the redshift at which galaxies collapse can be made using
the Jeans criterion: an overdensity larger
than MJ will stop expanding and collapse in a time
tc, given by
Taking the example of our own Milky Way, the total mass implied
from dynamical studies is 5 x 1011 M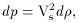
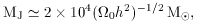
 0 is the
present mass density, and M is the unit of
solar mass (1 M
0 is the
present mass density, and M is the unit of
solar mass (1 M = 2
x 1030 kg).
= 2
x 1030 kg).
 106 yrs), the
energy density of the radiation field exceeds
that of the matter content and the sound speed is then relativistic.
During this period, known as the radiation dominated era, the minimum mass
required to undergo
gravitational collapse of baryonic overdensities rises to
106 yrs), the
energy density of the radiation field exceeds
that of the matter content and the sound speed is then relativistic.
During this period, known as the radiation dominated era, the minimum mass
required to undergo
gravitational collapse of baryonic overdensities rises to
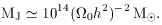
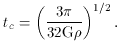
 and from the
distance
of the furthest stars in the galactic halo a plausible size to the Galaxy
before it collapsed is
and from the
distance
of the furthest stars in the galactic halo a plausible size to the Galaxy
before it collapsed is  100
kpc. This implies a density
3.6 x 10-24 kg m-3 and, using equation
(5) a collapse time
of
100
kpc. This implies a density
3.6 x 10-24 kg m-3 and, using equation
(5) a collapse time
of  109 yrs, which
corresponds to a look-back time of 7.2 Gyr if
109 yrs, which
corresponds to a look-back time of 7.2 Gyr if
 M =
0.2 and 5.4 Gyr if
M =
0.2 and 5.4 Gyr if  M
= 1.0 (all assuming
M
= 1.0 (all assuming

 = 0, h = 1). From
Figure 1 this
translates to redshifts of formation zf
= 0, h = 1). From
Figure 1 this
translates to redshifts of formation zf  4-2 respectively. If
h = 0.5 then formation redshifts range from zf
4-2 respectively. If
h = 0.5 then formation redshifts range from zf
 6-4 for the same
mass densities. Finally, bound objects the size of galaxies are unlikely to
exist much above these redshifts for the simple reason that the age of the
Universe is then short compared to the free-fall collapse time.
6-4 for the same
mass densities. Finally, bound objects the size of galaxies are unlikely to
exist much above these redshifts for the simple reason that the age of the
Universe is then short compared to the free-fall collapse time.