


8.2. Binary black hole formation
Given the large frequency of galaxy encounters and mergers, if there is a massive black hole in nearly every galaxy, the formation of a binary black hole should be a common phenomenon. The successive physical processes able to brake the two black holes in their relative orbit have been considered by Begelman et al (1980). Each black hole sinks first toward the merger remnant center through dynamical friction onto stars. A binary is formed; but the life-time of such a binary can be much larger than a Hubble time, if there is not enough stars to replenish the loss cone, where stars are able to interact with the binary. Once a loss cone is created, it is replenished only through the 2-body relaxation between stars, and this can be very long (see section 2). Modelising the merger remnant as an elliptical, with a core of radius rc and mass Mc (and corresponding velocity Vc), the radius where loss cone effects are significant is: rlc / rc = (Mbh / Mc)3/4. The various time-scales involved, and corresponding characteristic scales are defined by the following steps:
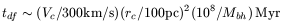
 (r / rb)3/2
(r / rb)3/2
All these time-scales are represented on figure 25. If the binary life-time is too long, another merger with another galaxy will bring a third black-hole. Since a three-body system is unstable, one of the three black-holes will be ejected by the gravitational slingshot effect.
Since the life-time of the binary is not short, there should be observable manifestations of massive black hole binaries. One of the best tracer is to detect the periodicity of the keplerian motion, with the period P ~ 1.6yr r163/2 M8-1/2. This is the case for the AGN OJ 287 where eclipses have been monitored for a century (Takalo 1994, Lehto & Valtonen 1996, Pietilä 1998). Also, if the black holes are rotating, and their spins have misaligned axes, they precess around the orbital one. Plasma beams (aligned to the hole axis) precess, and curved jets should be observed, with periods between 103 to 107 yr. This is frequently the case in radio structures observed with VLA and VLBI, modified by Doppler boosting, and light travel time (cf 3C 273, NGC 6251, 1928+738, Kaastra & Roos 1992; Roos et al 1993). Finally, pairs of radio galaxies have been observed during their merger with four radio jets (3C 75, Owen et al 1985).
Numerical simulations have brought more precision in the determination of the life-time of the binary, although numerical artifacts have given rise to debates. Ebisuzaki et al (1991) claimed that the life-time of the binary should be much shorter if its orbit is excentric, since then the binary can interact with more stars and release the loss cone problem. The first numerical simulations tended to show that orbit excentricity should grow quickly through dynamical friction (Fukushige et al 1992). Mikkola & Valtonen (1992) and others found that the excentricity in fact grows only very slowly.
Numerical simulations suffer from a restricted number of bodies N, and consequently of a large random velocity of the binary (that shoud decrease in N-1/2). The binary then wanders in or even out of the loss cone, and the effect of the loss cone depletion does not occur (Makino et al 1993). Also the 2-body relaxation time is shorter than in the real system, contributing to replenish the cone. Numerically, the life-time of the binary depends on the total number of particles, i.e. the ratio between the black hole to particle mass:
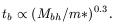
To summarize the conclusions of several numerical computations, there is finally little dependence on excentricity e, only in rare cases, when e is large from the beginning (Quinlan 1996). Eventually, the wandering of the binary helps the merging of the two black holes (Quinlan & Hernquist 1997). The ejection out of the core of stars interacting with the binary weakens the stellar cusp, while the binary hardens. This may help to explain the surprisingly weak stellar cusps in the center of giant ellipticals observed recently with HST. Observations show that bright elliptical galaxies have weak cusps, while faint galaxies have strong cusps, with a power law slope of density versus radius of up to 2. A way to weaken the cusps is a sinking black hole (Nakano & Makino 1999), and this could be the case for giant galaxies that have experienced many mergers in their life.