Annu. Rev. Astron. Astrophys. 1992. 30: 575-611 Copyright © 1992 by Annual Reviews. All rights reserved

4. SYNCHROTRON RADIATION

Synchrotron radiation from ultrarelativistic (E m_e c²) electrons dominates the radio emission from most normal galaxies at frequencies below ~ 30 GHz. Calculations of particle lifetimes, energy densities, etc. are more meaningful for the radio sources in normal galaxies than for sources in classical radio galaxies and quasars because (a) they may be compared with direct observations of cosmic rays in our galaxy and (b) equipartition between field and particle energy densities probably holds in normal galaxies (see Section 4.2). On the other hand, radio spectral signatures of cosmic-ray energy loss and transport processes are elusive, and tracing the cosmic rays to their sources is still difficult.

4.1 Basic Equations

Electrons with energy E moving at pitch angle in a magnetic field of strength B emit most of their energy near the critical frequency _c,

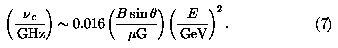
For a typical spiral disk field strength B ~ 5 µG, synchrotron emission in the 100:1 frequency range of 0.1-10 GHz is generated by electrons in the 10:1 energy range 1-10 GeV. The synchrotron power emitted by each electron is

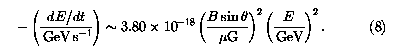
For isotropically distributed electron velocities, such as observed near the Sun, < sin² > = 2/3. The synchrotron lifetime _s E / |dE / dt| is

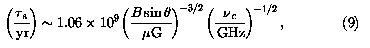
which is about 10⁸ yr at _c = 1.5 GHz for B = 5 µG. Inverse-Compton losses have the same energy dependence, and the ratio of synchrotron to inverse-Compton losses is equal to the ratio of magnetic energy density U_m = B² / (8) (U_m ~ 10^-12 erg cm^-3 in the Galaxy) to radiation energy density U_r. The components of U_r include the T = 2.7 (1 + z) K cosmic microwave background [U_r = aT⁴ ~ 4 x 10^-13(1 + z)⁴ erg cm^-3] and radiation from stars (U_r ~ 10^-12 cm^-3 in the Galaxy). The confinement time of cosmic rays in the solar neighborhood deduced from ¹⁰Be decay is ~ 2 x 10⁷ yr (Garcia-Munoz et al. 1977) or more (Dogiel 1990), so synchrotron and inverse-Compton losses may be significant at GHz frequencies. The radiation energy-density in compact (diameter D ~ 200 pc) ultraluminous [log (L_FIR / L) ~ 11.5, where L = 3.83 x 10²⁶ W] starbursts is so large (U_r ~ 3 x 10^-8 erg cm^-3) that the inverse-Compton lifetime of relativistic electrons emitting at ~ 10 GHz is only about 10⁴ yr (Condon et al. 1991c).

An ensemble of relativistic electrons can be described by the number density N(E)dE of electrons with energies between E and E+dE. If N(E) = N₀E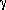^- and the electrons have an isotropic velocity distribution, their synchrotron emission coefficient is

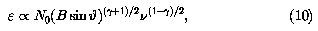
where is the angle between the magnetic field and the line of sight to the observer. The synchrotron radiation from an electron of energy E is confined to a beam of width ~ m_e c² / E 1 radian parallel to the electron velocity. An observer sees radiation exclusively from those electrons whose velocity vectors nearly cross his line-of-sight, so ~ and only the component of the magnetic field projected onto the sky plane contributes to the observed radiation. Thus, Equation 10 indicates that the observed brightness of a source depends on the direction of any ordered field component, even though the electrons are moving isotropically. For example, if the z-component of the magnetic field is significant in the halos of disk galaxies, synchrotron halos will appear brightest in edge-on systems and will be faintest in face-on systems (e.g. observations of our galaxy in directions near its pole).

Synchrotron self-absorption is only important for sources with brightness temperatures T_b > m_e c² / k ~ 10¹⁰ K, values apparently never attained by normal galaxies. The spectral index of the nonthermal emission from a normal galaxy is therefore = ( - 1) / 2. Usually, ~ 0.8 at GHz frequencies, implying ~ 2.6 at GeV energies.

Mathewson et al. (1972) stressed that the synchrotron emissivity is quite sensitive to changes in the magnetic field strength (i.e. 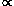B^{1 +} and hence to compression of the emitting volume containing both field and particles ( 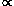x^{2 +} for a compression factor x). They ascribed bright ridges of synchrotron radiation coinciding with the dust lanes on the inner edges of spiral arms in M51 to compression of the interstellar medium (both particles and fields) by spiral arm shocks. Later maps made with higher resolution show that the nonthermal arm shapes are not consistent with simple compression (Tilanus et al. 1988): The nonthermal intensity gradients are steeper on the outside edge than on the inside edge, and the intensity peaks just inside the dust lanes. The gas containing the relativistic electrons does not appear to be shocked, possibly because its sound speed is the Alfvén speed, V_A = B / (4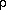)^1/2 ~ 100 km s^-1 in the hot ionized interstellar medium. In both M51 (Tilanus & Allen 1989) and M81 (Kaufman et al. 1989) the nonthermal arms are centered on the ridge of young stars and H II regions, not on the H I velocity shock front. Thus, star formation is more important than compression for producing radio spiral arms in normal galaxies.

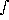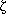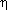If the production rate of relativistic electrons is q(E) and the total electron energy loss rate (E) depends on energy alone, then the equilibrium distribution of relativistic electrons is N(E) = ^-1 q(E) dE. The three terms in the approximation (E) = - - E - 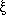E² correspond to ionization losses, relativistic bremsstrahlung plus adiabatic losses, and synchrotron plus inverse-Compton radiation, respectively. 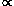For q(E) E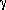_⁰, the equilibrium distribution of relativistic electrons is

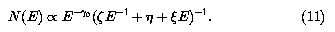
Because the ionization and bremsstrahlung loss rates have different energy dependences, bremsstrahlung losses exceed ionization losses at energies above the characteristic energy E ~ 0.3 GeV (for interstellar matter consisting primarily of hydrogen). The corresponding critical frequency in 5-10 µG fields is _c 10 MHz, so ionization losses in normal galaxies can usually be neglected. Relativistic bremsstrahlung losses in the disk of our galaxy are probably not severe since the cosmic-ray mean free path is ~ 5 g cm^-2 (Garcia-Munoz et al. 1977) ­ an order of magnitude smaller than the ~ 50 g cm² radiation length in the interstellar medium.

The combined synchrotron plus inverse-Compton losses exceed the relativistic bremsstrahlung plus adiabatic losses at energies E > 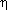/ 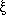, and the critical frequency (Equation 7) corresponding to E = 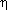/ 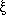is called the ``break'' frequency _b. With the approximation that relativistic electrons radiate only at their critical frequencies, Equation 11 yields for the nonthermal spectrum

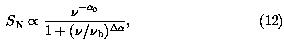
where ₀ (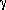₀ - 1) / 2 and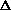 = 1 / 2 is the asymptotic change in spectral index. The spectral steepening from = ₀ to = ₀ + 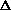is avidly sought by observers because _b might fall in the observable GHz frequency range. However, Equation 12 shows that this ``break'' is really only a very gradual bend, largely because _c 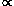E ² transforms a small energy range into a large frequency range. It is so gradual, unfortunately, that it is unobservable with the accuracy and frequency coverage of existing flux-density measurements of normal galaxies. This point is illustrated by the two model spectra in Figure 6. Werner (1988) describes the related difficulty of distinguishing changes in ₀ from changes in _b in the spectrum of NGC 4631. Nonetheless, a spectral steepening consistent with 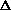~ 0.5 with z in the disk/halo spectra of the edge-on galaxies NGC 891 and NGC 4631 has been reported (Hummel 1991b).

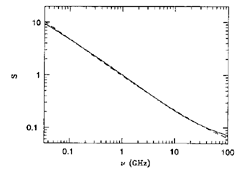Figure 6. The continuous curve is the spectrum of a galaxy with 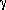₀ = 2.2, spectral bend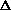 = 1/2 centered on _b = 5 GHz, and thermal/nonthermal flux ratio S_T / S_N = 0.1 at = 1 GHz. The broken curve corresponds to a power-law nonthermal spectrum with = 0.71 plus a weaker thermal contribution S_T / S_N = 0.05 at = 1 GHz. The spectral bend caused by synchrotron and inverse-Compton losses is too gradual for these spectra to be distinguished observationally. Abscissa: frequency (GHz). Ordinate: relative flux density (arbitrary units).