

© CAMBRIDGE UNIVERSITY PRESS 1998
| |
1.5 Spectroscopy of Systems of Light Quarks
As will be discussed in Chapter 16, the masses of the u and d quarks
are quite small, of the order of a few MeV / c2,
closer to the electron
mass than to a meson or baryon mass. A u or d quark confined within a
distance  1 fm has, by the
uncertainty principle, a momentum p
1 fm has, by the
uncertainty principle, a momentum p 
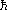 / (1 fm)
/ (1 fm)  200 MeV / c, and hence its
energy is E
200 MeV / c, and hence its
energy is E  pc
pc
 200 MeV, almost
independent of the quark mass. All quarks have the same strong
interactions. As a consequence the physics of light quark systems is
almost independent of the quark masses. There is an approximate
SU (2)
isospin symmetry (Section 16.6), which is evident in the Standard Model.
200 MeV, almost
independent of the quark mass. All quarks have the same strong
interactions. As a consequence the physics of light quark systems is
almost independent of the quark masses. There is an approximate
SU (2)
isospin symmetry (Section 16.6), which is evident in the Standard Model.
The symmetry is not exact because of the different quark masses and different quark charges. The symmetry breaking due to quark mass differences prevails over the electromagnetic. In all cases where two particles differ only in that a d quark is substituted for a d quark, the particle with the d quark is more massive. For example, the neutron is more massive than the proton, even though the mass, ~ 2 MeV / c2, associated with the electrical energy of the charged proton is far greater than that associated with the (overall neutral) charge distribution of the neutron. We conclude that the d quark is heavier than the u quark.
The evidence for the existence of quarks came first from nucleon spectroscopy. The proton and neutron have many excited states which appear as resonances in photon-nucleon scattering and in pion-nucleon scattering (Fig. 1.1). Hadron states containing light quarks can be classified using the concept of isospin. The u and d quarks are regarded as a doublet of states | u> and | d>, with I = 1/2 and I3 = + 1/2, - 1/2, respectively. The total isospin of a baryon made up of three u or d quarks is then I = 3/2 or I = 1/2. The isospin 3/2 states make up multiplets of four states almost degenerate in energy but having charges 2e(uuu), e(uud), 0(udd), - e(ddd). The I = 1/2 states make up doublets, like the proton and neutron, having charges e(uud) and 0(udd). The electric charge assignments of the quarks were made to comprehend this baryon charge structure.
Energy level diagrams of the I = 3/2 and I = 1/2 states up to
excitation energies of 1 GeV are shown in
Fig. 1.2. The energy
differences between states in a multiplet are only of the order of 1
MeV and cannot be shown on the scale of the figure. The widths  of
the excited states are however quite large, of the order of 100 MeV,
corresponding to mean lives
of
the excited states are however quite large, of the order of 100 MeV,
corresponding to mean lives  =
= 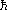 /
/  ~ 10-23 s. The excited states are
all energetic enough to decay through the strong interaction, as for
example
~ 10-23 s. The excited states are
all energetic enough to decay through the strong interaction, as for
example  ++ -> p +
++ -> p +
 +
(Fig. 1.3).
+
(Fig. 1.3).
The rich spectrum of the baryon states can largely be described and
understood on the basis of a simple ``shell'' model of three confined
quarks. The lowest states have orbital angular momentum L = 0 and
positive parity. The states in the next group have L = 1 and negative
parity, and so on. However, the model has the curious feature that, to
fit the data, the states are completely symmetric in the interchange
of any two quarks. For example, the  ++(uuu), which belongs to the
lowest I = 3/2 multiplet, has Jp =
3/2+. If L = 0 the three quark
spins must be aligned
++(uuu), which belongs to the
lowest I = 3/2 multiplet, has Jp =
3/2+. If L = 0 the three quark
spins must be aligned 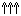 in a symmetric state to give J = 3/2, and
the lowest energy spatial state must be totally symmetric. Symmetry
under interchange is not allowed for an assembly of identical
fermions! However, there is no doubt that the model demands symmetry,
and with symmetry it works very well. The resolution of this problem
will be left to later in this chapter. There are only a few states
(broken lines in Fig. 1.2) which cannot be
understood within the simple shell model.
in a symmetric state to give J = 3/2, and
the lowest energy spatial state must be totally symmetric. Symmetry
under interchange is not allowed for an assembly of identical
fermions! However, there is no doubt that the model demands symmetry,
and with symmetry it works very well. The resolution of this problem
will be left to later in this chapter. There are only a few states
(broken lines in Fig. 1.2) which cannot be
understood within the simple shell model.
| Quark | Isospinl | I3 |
| u | 1/2 | 1/2 |
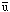 | 1/2 | -1/2 |
| d | 1/2 | -1/2 |
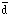 | 1/2 | 1/2 |
| s | 0 | 0 |
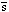 | 0 | 0 |
Mesons made up of light u and d quarks and their antiquarks also
have a rich spectrum of states which can be classified by their
isospin. Antiquarks have an I3 of opposite sign to
that of their
corresponding quark (Table 1.4). By the rules
for the addition of
isospin, quark-antiquark pairs have I = 0 or I = 1. The
I = 0 states
are singlets with charge 0, like the  (Fig. 1.4(a)). The
I = 1 states
make up triplets carrying charge +e, 0, -e, which are almost
degenerate in energy, like the triplet
(Fig. 1.4(a)). The
I = 1 states
make up triplets carrying charge +e, 0, -e, which are almost
degenerate in energy, like the triplet  +,
+,  0,
0,  -.
-.
The spectrum of I = 1 states with energies up to 1.5 GeV is shown in Fig. 1.4(b). As in the baryon case the splitting between states in the same isotopic multiplet is only a few MeV; the widths of the excited states are like the widths of the excited baryon states, of the order of 100 MeV. In the lowest multiplet (the pions), the quark-antiquark pair is in an L = 0 state with spins coupled to zero. Hence Jp = 0-, since a fermion and antifermion have opposite relative parity (Section 6.4). In the first excited state the spins are coupled to 1 and Jp = 1-. These are the p mesons. With L = 1 and spins coupled to S = 1 one can construct states 2+, 1+, 0+, and with L = 1 and spins coupled to S = 0 a state 1+. All these states can be identified in Fig. 1.4(b).