


3.3. Cosmic Virial Theorem
In the cosmic virial theorem (CVT), clustering is assumed to be
statistically stable on scales
 1
h-1Mpc, such that the ensemble-average
contribution of a third mass particle to the relative acceleration of
a pair of galaxies is balanced by the relative motions of the ensemble of
pairs. The kinetic energy is represented
by the pairwise relative velocity dispersion of galaxies
[
1
h-1Mpc, such that the ensemble-average
contribution of a third mass particle to the relative acceleration of
a pair of galaxies is balanced by the relative motions of the ensemble of
pairs. The kinetic energy is represented
by the pairwise relative velocity dispersion of galaxies
[ 12(r)],
and the potential energy involves a combination of integrals of the
2- and 3-point galaxy correlation functions
[26].
A very crude approximation to the actual relation is
12(r)],
and the potential energy involves a combination of integrals of the
2- and 3-point galaxy correlation functions
[26].
A very crude approximation to the actual relation is
where
On scales 1 - 10 h-1Mpc the more useful
statistics for dynamical mass estimates
is the mean (first moment) pairwise velocity in comparison with an integral
of the galaxy two-point correlation function.
In the approach of the Layzer-Irvine (LI) equation,
the kinetic energy is associated
with the absolute rms velocity (in the CMB frame) of
individual galaxies and the potential energy is an integral over
the 2-point correlation function.
New developments:
It has been realized that the pair velocity dispersion
is an unstable statistic that is dominated by galaxies in clusters.
Attempts are being made to apply the method while excluding clusters.
Pro:
There is no need to associate galaxies with separate groups and clusters;
it is all statistical.
Con:
The relevant correlation integrals, and in particular the 3-point
correlation function that enters the CVT, are very difficult to measure.
Current Results:
The line-of-sight pair velocity dispersion outside of clusters is in the
range
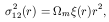
 (r) is the
two-point correlation function. In some ways this is like
stacking many groups of galaxies to get a mean M/L,
so it can be regarded as a statistical version of the mass-to-light
ratio method.
(r) is the
two-point correlation function. In some ways this is like
stacking many groups of galaxies to get a mean M/L,
so it can be regarded as a statistical version of the mass-to-light
ratio method.
 Filtered versions of the LI approach help truncate the
(weak) divergence in estimating the potential energy and make the kinetic
energy term easier to estimate from data.
Filtered versions of the LI approach help truncate the
(weak) divergence in estimating the potential energy and make the kinetic
energy term easier to estimate from data.
 In the LI method the energies are dominated by contributions from the
large-scale mass distribution, and it is therefore less contaminated
by clusters and less biased by the assumption of point masses.
The two-point correlation for the LI method can be measured with
reasonable accuracy.
In the LI method the energies are dominated by contributions from the
large-scale mass distribution, and it is therefore less contaminated
by clusters and less biased by the assumption of point masses.
The two-point correlation for the LI method can be measured with
reasonable accuracy.
 The pair velocity dispersion in the CVT is an unstable statistic,
that is dominated
by pairs of galaxies in clusters. A robust, self-consistent way to avoid
the clusters is yet to be found.
The pair velocity dispersion in the CVT is an unstable statistic,
that is dominated
by pairs of galaxies in clusters. A robust, self-consistent way to avoid
the clusters is yet to be found.
 The absolute velocity dispersion which enters the LI equation
is hard to measure.
The absolute velocity dispersion which enters the LI equation
is hard to measure.
 The CVT assumes that galaxies are point masses (or of finite size),
which overestimates the force that they exert, and biases
The CVT assumes that galaxies are point masses (or of finite size),
which overestimates the force that they exert, and biases
 m low.
The overlap of extended galactic halos makes a significant difference.
m low.
The overlap of extended galactic halos makes a significant difference.
 The methods depend on the assumption that the statistical
distribution of galaxies and mass are similar (as in the
M/L method).
Otherwise, they must refer to a specific model for galaxy biasing.
The methods depend on the assumption that the statistical
distribution of galaxies and mass are similar (as in the
M/L method).
Otherwise, they must refer to a specific model for galaxy biasing.
 f
f
 300 ± 100 km
s-1
[27]
[28].
With Peebles' old estimate of the correlation functions, assuming point
masses and no biasing, he obtains from the CVT
300 ± 100 km
s-1
[27]
[28].
With Peebles' old estimate of the correlation functions, assuming point
masses and no biasing, he obtains from the CVT
 m
m
 0.15
[6].
0.15
[6].
 From
the mean pairwise velocity in IRAS 1.2Jy
[27]:
From
the mean pairwise velocity in IRAS 1.2Jy
[27]:
 m ~ 0.25.
m ~ 0.25.
 However, it has been demonstrated that with an extended mass distribution
in galactic halos the above CVT estimates are lower bounds,
and that the observations may be consistent with
However, it has been demonstrated that with an extended mass distribution
in galactic halos the above CVT estimates are lower bounds,
and that the observations may be consistent with
 m
m
 1
[29].
1
[29].