


7.5 Statistical Masses
The loose structure of most nearby groups does not inspire confidence in their stability or in the validity of total masses derived from velocily dispersion through the virial theorem (Local Group: Humason and Wahlquist 1953, Kahn and Woltjer 1959, Godfredsen 1961; Sculptor group: de Vaucouleurs 1959; M81 group: Holmberg 1950, Ambartsumian 1958, Limber 1961; CVn cluster: van den Bergh 1960d; Virgo Cluster: Oort 1958, van den Bergh 1960d, Holmberg 1961, de Vaucouleurs 1961c; NGC 5846 group: de Vaucouleurs 1960a; see also Neyman, Page, and Scott 1961). (3)
Although the evidence is perhaps not yet completely conclusive, the overall impression gained from extensive discussions of this topic is that while large, centrally condensed clusters of the Coma type are probably sufficiently relaxed and stable over periods of time long enough to justify an application of the virial theorem, the same cannot be said of the majority of nearby groups and clouds with the possible exceptions of the E components of the Virgo I and Fornax I clusters. Hence masses derived from velocity dispersion are probably meaningless.
| Average | Nearer Groups | All Groups | Clouds | Clusters* |
| Number of groups | 10 | 27 | 13 | 3 |
Velocity dispersion  v (km/sec) v (km/sec)
| 100** | 200 | 250 | 650: |
| Radius R (Mpc) | 0.4 | 0.4 | 0.6 | 0.6: |
Total mass MT (1011
M ) )
| 40 | 160 | 480 | 3000: |
Mass per galaxy M1 (1011
M )*** )***
| 2 | 5 | 3 | 12: |
Density  (10-27 g cm-3)
(10-27 g cm-3)
| 2 | 5 | 3 | 24: |
* Vir I (E), Vir I (S), For I.
** Approx. corrected for observational errors.
*** Assuming NT 10 N18 in first 5
magnitudes.
There is, therefore, little point in applying the virial theorem to each of the 55 nearby groups and clouds. It should be sufficient to list the average masses and densities that would result from a conventional application of the standard method to the mean of all nearby groups and clouds.
The calculations use the crude but sufficient approximation
MT
3 For more recent discussions see
Rood et al. (1970)
and Geller and Peebles (1973).
Back.
 5 R
5 R v2 / G, where R
v2 / G, where R

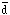 / 4, if
/ 4, if
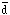 = mean major diameter of groups,
and
= mean major diameter of groups,
and  v
v
 2
2  ) and
from the virial theorem (~ 1011-1012
M
) and
from the virial theorem (~ 1011-1012
M ). It is more
pronounced for
the three clusters than for groups or clouds. Rejection of possible
foreground or background objects in Virgo reduces the discrepancy only
slightly
(de Vaucouleurs 1961c;
Holmberg 1961).
). It is more
pronounced for
the three clusters than for groups or clouds. Rejection of possible
foreground or background objects in Virgo reduces the discrepancy only
slightly
(de Vaucouleurs 1961c;
Holmberg 1961).