


If we have a sample with distance information for every object, so
that we know L(r, S) = 4  r2 S for each galaxy, we can define a volume
over which the sample is complete to any arbitrarily low luminosity,
and compute the density of galaxies as a function of luminosity. This
is the approach taken by
Schechter (1976),
using a sample from the
Reference Catalog of Bright Galaxies
(de Vaucouleurs and
de Vaucouleurs 1967)
which is magnitude limited at B0 = 11.75. An
alternative method to derive n(L) is to study rich clusters which are
distant enough that 1 / r2 is roughly constant for all
members and rich
enough that confusion due to foreground and background galaxies in the
field is not a major problem
(Oemler 1974).
A compendium of various functional forms for n(L) is given by
Felten (1977).
The form chosen
by Press and
Schechter (1974)
is very popular, not because it is
simple, but because it follows from a theoretical analysis of
self-similar gravitational condensation in the early universe. This is
a three parameter function of the form:
r2 S for each galaxy, we can define a volume
over which the sample is complete to any arbitrarily low luminosity,
and compute the density of galaxies as a function of luminosity. This
is the approach taken by
Schechter (1976),
using a sample from the
Reference Catalog of Bright Galaxies
(de Vaucouleurs and
de Vaucouleurs 1967)
which is magnitude limited at B0 = 11.75. An
alternative method to derive n(L) is to study rich clusters which are
distant enough that 1 / r2 is roughly constant for all
members and rich
enough that confusion due to foreground and background galaxies in the
field is not a major problem
(Oemler 1974).
A compendium of various functional forms for n(L) is given by
Felten (1977).
The form chosen
by Press and
Schechter (1974)
is very popular, not because it is
simple, but because it follows from a theoretical analysis of
self-similar gravitational condensation in the early universe. This is
a three parameter function of the form:
where the parameters are n (the total density),
An analog to the median luminosity galaxy is the ``half-light"'' object,
for which half the total luminosity of the sample comes from galaxies
of higher luminosity, half from lower:
which gives L1/2 = 0.16 L
we find M
If the parameters
Another question about the optical luminosity function which is
currently discussed is whether different luminosity functions should
be used for different galaxy types
(Sandage et al. 1985,
Binggeli 1987).
If dwarf ellipticals and ordinary ellipticals are considered
separately, the luminosity function of the larger galaxies is
typically Gaussian; the same is true for irregulars and spirals.
Virgo
is the only cluster for which we have complete catalogs of galaxies
faint enough to measure various luminosity functions for different
galaxy types. It is known in many clusters that the relative abundance
of different galaxy types is a strong function of the local density of
galaxies
(Dressler 1980),
so it is not implausible that at least
ellipticals and spirals might have different luminosity
functions. This is certainly true at the very high end, where the
(exclusively elliptical) cD's are often so far above L
Assuming that different galaxy types have distinct luminosity
functions, morphological segregation (e.g.,
Giovanelli and Haynes
1985,
Dressler 1980)
appears to require that the overall galaxy
luminosity function vary with position, since varying the relative
fractions of spiral, elliptical and S0 galaxies varies the
contribution of each of their luminosity functions to the aggregate
luminosity function. Since the colors of galaxies also correlate with
type this means that the aggregate Schechter function parameters must
also vary with color. Large scale structure in the galaxy
distribution entails more than a variation in n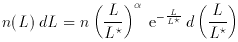
 (the power law slope
for very low L), and L
(the power law slope
for very low L), and L (the luminosity of the ``break'' where the slope
of n(L) changes rapidly). For L greater than L
(the luminosity of the ``break'' where the slope
of n(L) changes rapidly). For L greater than L , n(L) decreases
exponentially. Typical values for
, n(L) decreases
exponentially. Typical values for  lie in the range -1.5 <
lie in the range -1.5 <  < -1, so
integrating over all luminosities the total number of galaxies
diverges. This is not necessarily unphysical, since the total
luminosity,
< -1, so
integrating over all luminosities the total number of galaxies
diverges. This is not necessarily unphysical, since the total
luminosity,  L
n(L) dL remains finite. Integrals of the Schechter
function can often be expressed in terms of the incomplete gamma
function
(Davis 1964), e.g.,
L
n(L) dL remains finite. Integrals of the Schechter
function can often be expressed in terms of the incomplete gamma
function
(Davis 1964), e.g.,
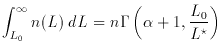
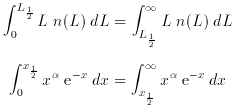
 , i.e., about 2 magnitudes fainter than L
, i.e., about 2 magnitudes fainter than L .
Expressing the luminosity parameter as a magnitude
.
Expressing the luminosity parameter as a magnitude
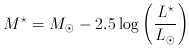
 typically
has a value in the range -23 < M
typically
has a value in the range -23 < M + 5 log h50 <-20
in the blue.
+ 5 log h50 <-20
in the blue.
 and
L
and
L of the Schechter
function were
independent of position (i.e., a global form for the luminosity
function varying only in its normalization, n), then many problems
could be greatly simplified. For example, distances to clusters could
be estimated by measuring the number of galaxies vs. apparent
magnitude, and fitting L
of the Schechter
function were
independent of position (i.e., a global form for the luminosity
function varying only in its normalization, n), then many problems
could be greatly simplified. For example, distances to clusters could
be estimated by measuring the number of galaxies vs. apparent
magnitude, and fitting L . (A more sophisticated treatment of this
idea is given by
Schechter and Press
1976.)
The variation of the
luminosity function among clusters has been studied by
Dressler (1978)
and more recently by
Lugger (1986).
Apparently there is variation of
almost two magnitudes in M
. (A more sophisticated treatment of this
idea is given by
Schechter and Press
1976.)
The variation of the
luminosity function among clusters has been studied by
Dressler (1978)
and more recently by
Lugger (1986).
Apparently there is variation of
almost two magnitudes in M from cluster to cluster, although this
variation is not clearly associated with cluster properties; in
particular the presence of a cD does not imply a depletion of moderate
luminosity galaxies, supporting
Merritt's (1985)
conclusion that cD's
are not growing significantly by cannibalism at present. It remains an
open question whether either the parameters L
from cluster to cluster, although this
variation is not clearly associated with cluster properties; in
particular the presence of a cD does not imply a depletion of moderate
luminosity galaxies, supporting
Merritt's (1985)
conclusion that cD's
are not growing significantly by cannibalism at present. It remains an
open question whether either the parameters L and
and  , or the form of
the luminosity function itself, vary with large scale environment,
e.g., between clusters and voids. This would be expected in a ``biased
galaxy formation'' scenario (e.g.,
Dekel and Silk 1986)
where the initial mass function of galaxies is strongly influenced by the local
mass density.
, or the form of
the luminosity function itself, vary with large scale environment,
e.g., between clusters and voids. This would be expected in a ``biased
galaxy formation'' scenario (e.g.,
Dekel and Silk 1986)
where the initial mass function of galaxies is strongly influenced by the local
mass density.
 that their
abundance is not well fit by the exponential cutoff of the Schechter
function at the high end.
that their
abundance is not well fit by the exponential cutoff of the Schechter
function at the high end.
 with position; in
fact we may need a multivariate luminosity function, for example
n(L,
with position; in
fact we may need a multivariate luminosity function, for example
n(L,  ) where
) where  is the density of
galaxies in the immediate
environment. Data which could be used to derive this function are
presented by Haynes in this volume.
is the density of
galaxies in the immediate
environment. Data which could be used to derive this function are
presented by Haynes in this volume.