
DARK MATTER, COSMOLOGICAL
Edmund Bertschinger
Dark matter is mass that does not emit or reflect detectable electromagnetic radiation, yet is detectable by its gravitational effect on other, luminous, matter. Perhaps 90% or more of all the matter in the universe is dark. Dark matter has been inferred to exist in galaxies and on larger scales in the universe, but not in the solar system. The nature and total amount of dark matter are unknown, although there are constraints from astronomical observations and particle physics experiments. The abundance, distribution, and nature of dark matter are outstanding questions in modern cosmology.
The total abundance of dark matter has important implications for
the evolution of the universe. If the mean density is large enough,
dark matter can close the universe, causing the universal Hubble
expansion eventually to halt and reverse. For cosmological purposes,
the most convenient way to express the abundance of some type of mass
labeled i is by the ratio of the mean mass density  i of that
substance to the mean mass density
i of that
substance to the mean mass density  crit, required to close the universe:
crit, required to close the universe:
The critical density depends on the gravitational constant G and the
Hubble constant H0 = 100 h km s-1
Mpc-1. The Hubble constant is poorly
known, but nearly all modern estimates give 0.5 < h < 1.0. If the total
density parameter
To place the abundance question in perspective, it is useful to
compare the mean density of dark matter with that of luminous
matter-stars and gas in galaxies and galaxy clusters -
The first measurement of dark matter in the Galaxy was made by Jan
Oort in 1932, who concluded that visible stars near the sun could
account for only about half the mass implied by the velocities of
stars perpendicular to the disk of our Galaxy. In 1933, Fritz Zwicky
applied a similar dynamical argument to clusters of galaxies, noting
that observed galaxies accounted for 10% or less of the mass needed to
gravitationally bind clusters, given the large velocities of galaxies
in a cluster. For a self-gravitating system in equilibrium, the mass
is M
The most straightforward and extensive mass measurements have been
made for spiral galaxies, for which V is the circular rotation speed
at radius R and M is the mass interior to R. The
rotation curve V (R)
has been measured for hundreds of spirals, using the Doppler shift of
the optical H
Gravitational mass measurements have also been performed for
elliptical galaxies, small groups, and rich clusters of galaxies.
These measurements are less certain than those for spirals, largely
because of the uncertainty of the distribution of stellar or galactic
orbits in the systems analyzed. X-ray emission from hot gas in
hydrostatic equilibrium in clusters should allow more precise
determinations once accurate gas temperature measurements become
available. The mass measurements of ellipticals, groups, and clusters
confirm the existence of dark matter and increase the estimated total
Because galaxies and clusters occupy a small fraction of the volume
of the universe, measurements on larger length scales are needed to
obtain the total mean density in dark matter. Unfortunately,
equilibrium structures larger than galaxy clusters do not exist, so
that large-scale gravitational mass density measurements cannot be
based on the simple formula M
It is possible to measure
Many important theoretical questions are raised by the existence of
dark matter. Perhaps the most obvious are: What is it? Is it baryonic?
This possibility is marginally allowed if
If the dark matter is nonbaryonic, it probably consists of
elementary particles without electromagnetic or strong interactions;
for otherwise it should have been detected by now. There is no
shortage of possible candidates proposed by particle physicists,
although none except the neutrino are known to exist. Most of these
dark matter candidates undergo weak nuclear interactions, so it should
be possible to detect them in laboratory experiments of sufficient
sensitivity. A key implication of the dark matter hypothesis is that
these particles should be abundant in every laboratory on the Earth,
with a flux ~ 102 cm-2 s-1 if the
particle has mass comparable to a
proton. Many experiments are underway to try to detect these
particles.
From an astrophysical point of view, most of the properties of The
dark matter are irrelevant. The one significant detail is the
temperature of the dark matter distribution. Cold dark matter (CDM)
particles have negligible random velocities before the epoch of galaxy
formation, while hot dark matter (HDM) is hot enough to evaporate
(erase by free streaming) galaxy-scale primordial density
perturbations. Cosmological scenarios with hot and cold dark matter
differ in that, in the former, galaxy formation occurs only after the
fragmentation of cluster-or supercluster-sized sheets of collapsed
matter (``pancakes''), whereas in the CDM model, galaxy formation and
clustering proceeds hierarchically, with small objects merging to form
larger ones. The latter scenario appears to be more consistent with
the relative ages of galaxies and superclusters, but no model is
entirely successful. Another problem with HDM is that it cannot
cluster enough to provide the dark matter in dwarf galaxies. The
best-known HDM candidate is a neutrino with mass ~
20h-2 eV c-2, for
example, the tau neutrino, whose experimental mass limit allows this
possibility. The most widely discussed CDM candidates are axions,
invoked to solve problems in the theory of quantum chromodynamics, and
the lightest supersymmetric particle, which is predicted to be
stable. Theories of unstable dark matter or of two or more types of
dark matter have been advanced occasionally but they are not as
appealing as the simple models with one stable dark matter particle.
 i
i 
 i /
i /  crit = 8
crit = 8 G
G i /
3H02;
i /
3H02;
 crit =
1.9 x 10-29 h2 g cm-3
crit =
1.9 x 10-29 h2 g cm-3
 from all
types of matter exceeds 1, the universe
is closed and will eventually collapse. If
from all
types of matter exceeds 1, the universe
is closed and will eventually collapse. If  < 1, the universe will
continue expanding forever. The inflationary universe model of Big
Bang cosmology predicts that
< 1, the universe will
continue expanding forever. The inflationary universe model of Big
Bang cosmology predicts that  = 1 to high precision, but this idea has
not been confirmed by observations. Observational estimates yield a
total
= 1 to high precision, but this idea has
not been confirmed by observations. Observational estimates yield a
total 
 0.1-1, with some preference for
smaller values (
0.1-1, with some preference for
smaller values (
 0.2).
0.2).
 lum
lum  0.01h-1. It
is plausible that most of the ordinary, baryonic matter (with atomic
nuclei made of baryons, i.e., protons and neutrons) in the universe
does not emit radiation detectable using present technology. For
example, planets, brown dwarfs, cold white dwarfs, neutron stars, and
intergalactic gas are difficult to detect at large distances, although
they are not dark in principle. Baryonic matter in these forms could
increase the total baryonic density parameter to
0.01h-1. It
is plausible that most of the ordinary, baryonic matter (with atomic
nuclei made of baryons, i.e., protons and neutrons) in the universe
does not emit radiation detectable using present technology. For
example, planets, brown dwarfs, cold white dwarfs, neutron stars, and
intergalactic gas are difficult to detect at large distances, although
they are not dark in principle. Baryonic matter in these forms could
increase the total baryonic density parameter to  b
b  0.05-0.10. Support for
this possibility comes from the theory of primordial nucleosynthesis,
which predicts the abundance of the light isotopes of hydrogen,
helium, and lithium produced during the first three minutes after the
Big Bang. Excellent agreement with measurements is obtained for
0.05-0.10. Support for
this possibility comes from the theory of primordial nucleosynthesis,
which predicts the abundance of the light isotopes of hydrogen,
helium, and lithium produced during the first three minutes after the
Big Bang. Excellent agreement with measurements is obtained for
 b = (0.02
± 0.01)h-2.
b = (0.02
± 0.01)h-2.
OBSERVATIONAL EVIDENCE FOR DARK MATTER
 RV2 / G, where R is the characteristic
size of the system and V is
the characteristic velocity of stars or other test bodies in the
system.
RV2 / G, where R is the characteristic
size of the system and V is
the characteristic velocity of stars or other test bodies in the
system.
 line or the
radio 21-cm line of hydrogen. In almost all
cases, V (R) is nearly constant outside of the galactic nucleus,
indicating a mass increasing linearly with radius or a density
decreasing with the inverse square of the radius. Since the luminosity
density typically decreases exponentially with radius, the
mass-to-light ratio becomes large in the outer parts, implying that
spiral galaxies are embedded in halos of dark matter. For our own
Galavy, with V
line or the
radio 21-cm line of hydrogen. In almost all
cases, V (R) is nearly constant outside of the galactic nucleus,
indicating a mass increasing linearly with radius or a density
decreasing with the inverse square of the radius. Since the luminosity
density typically decreases exponentially with radius, the
mass-to-light ratio becomes large in the outer parts, implying that
spiral galaxies are embedded in halos of dark matter. For our own
Galavy, with V  220
km s-1, M could be as large as 1012 solar
masses if the halo extends to 100 kpc. Adopting a mean separation of
5h-1 Mpc,
220
km s-1, M could be as large as 1012 solar
masses if the halo extends to 100 kpc. Adopting a mean separation of
5h-1 Mpc,  in bright spirals alone is ~ 0.03.
in bright spirals alone is ~ 0.03.
 in galaxies and clusters to
~ 0.1-0.2. Similar results follow from
the cosmic virial theorem, a statistical method based on the relative
velocities of all close pairs of galaxies.
in galaxies and clusters to
~ 0.1-0.2. Similar results follow from
the cosmic virial theorem, a statistical method based on the relative
velocities of all close pairs of galaxies.
 RV2 / G. Instead, cosmologists apply the
linear theory of gravitational instability in an expanding universe,
supposing that the mass density fluctuations have small amplitude on
large scales. The mass density is written
RV2 / G. Instead, cosmologists apply the
linear theory of gravitational instability in an expanding universe,
supposing that the mass density fluctuations have small amplitude on
large scales. The mass density is written  =
= 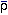 +
+ 
 , where
, where 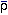 is the mean
density and
is the mean
density and 
 /
/ 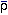 is the
spatially varying relative density
fluctuation. When smoothed on the scale of superclusters of galaxies,
is the
spatially varying relative density
fluctuation. When smoothed on the scale of superclusters of galaxies,

 /
/ 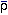 should be,
according to theory, related to the ``peculiar''
velocity field - the velocity remaining after the Hubble velocity of
uniform cosmological expansion is subtracted - with a constant of
proportionality depending on
should be,
according to theory, related to the ``peculiar''
velocity field - the velocity remaining after the Hubble velocity of
uniform cosmological expansion is subtracted - with a constant of
proportionality depending on  . Measurements of
. Measurements of  based on this
relation have yielded values in the range 0.2 to 1, with a preference
for small values. However, this technique suffers from a major
problem. The net density contrast
based on this
relation have yielded values in the range 0.2 to 1, with a preference
for small values. However, this technique suffers from a major
problem. The net density contrast 
 /
/
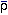 must be
known, but the density
on large scales is dominated by the unseen dark matter. In practice
the assumption is usually made that on large scales dark and luminous
matter are distributed similarly, so that
must be
known, but the density
on large scales is dominated by the unseen dark matter. In practice
the assumption is usually made that on large scales dark and luminous
matter are distributed similarly, so that 
 /
/ 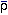 =
=  ng /
ng / 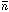 g, where
g, where
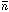 g +
g +  ng is the
smoothed galaxy density. However, there is no
empirical evidence supporting this assumption, and there are sound
theoretical arguments suggesting that the galaxy distribution should
be biased with respect to the dark matter distribution. In the
simplest theoretical model, the galaxy distribution has a density
contrast larger by a factor b, called the bias parameter, than the
matter distribution:
ng is the
smoothed galaxy density. However, there is no
empirical evidence supporting this assumption, and there are sound
theoretical arguments suggesting that the galaxy distribution should
be biased with respect to the dark matter distribution. In the
simplest theoretical model, the galaxy distribution has a density
contrast larger by a factor b, called the bias parameter, than the
matter distribution:  ng /
ng / 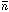 g = b(
g = b(
 /
/ 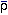 ). If b = 2.5, then the
apparent
). If b = 2.5, then the
apparent  could be ~ 0.2, whereas the true
could be ~ 0.2, whereas the true  = 1. This possibility is favored by
theorists who advocate the inflationary-universe model, but presently
is a conjecture neither confirmed nor refuted by observations.
= 1. This possibility is favored by
theorists who advocate the inflationary-universe model, but presently
is a conjecture neither confirmed nor refuted by observations.
 on still larger scales, by computing
the rate of deceleration of the Hubble expansion using observations of
cosmologically distant objects. There are a variety of methods for
accomplishing this, but all those employed to date suffer from large
uncertainties of the structure and cosmological evolution of the
objects studied.
on still larger scales, by computing
the rate of deceleration of the Hubble expansion using observations of
cosmologically distant objects. There are a variety of methods for
accomplishing this, but all those employed to date suffer from large
uncertainties of the structure and cosmological evolution of the
objects studied.
THEORETICAL ISSUES

 0.1, being consistent
with primordial nucleosynthesis for h = 0.5 and with most dynamical
determinations. However, the isotropy of the cosmic microwave
background radiation imposes theoretical constraints on baryonic dark
matter models that are difficult to satisfy.
0.1, being consistent
with primordial nucleosynthesis for h = 0.5 and with most dynamical
determinations. However, the isotropy of the cosmic microwave
background radiation imposes theoretical constraints on baryonic dark
matter models that are difficult to satisfy.
Faber, S.M. and Gallagher, J.S. (1979). Mass and mass-to-light
ratios of galaxies Ann. Rev. Astron. Ap. 17 135.
Krauss, L.M. (1986). Dark matter in the universe.
Scientific American 255 (No. 6) 58.
Peebles, P.J.E. (1986). The mean mass density of the Universe.
Nature 321 27.
Rubin, V.C. (1983). Dark matter in spiral galaxies.
Scientific American 248 (No. 6) 96.
Trimble, V. (1987). Existence and nature of dark matter in the
Universe. Ann. Rev. Astron. Ap. 25 425.
Tucker, W. and Tucker, K. (1988). The Dark Matter. William
Morrow and Co., New York.
See also Cosmology, Galaxy Formation; Cosmology, Theories.