GRAVITATIONAL RADIATION
Stephen P. Boughn
In the language of Albert Einstein's general theory of relativity, gravitational radiation or gravitational waves (GWs) are ``ripples in the geometry of space and time.'' A less abstruse way to describe gravitational radiation is by drawing an analogy to the electromagnetic spectrum (light, infrared, radio, microwave, x-ray, etc.). Just as these represent forms of the free radiation or waves associated with electricity and magnetism, so GWs represent the radiation associated with the force of gravity. Einstein actually predicted their existence in 1916, the same year his paper on general relativity theory was published. He even calculated the radiation emitted from a binary star system (the strongest source known at the time) and concluded that the radiation was so weak that it had ``a negligible practical effect.'' For the next half century gravitational radiation remained a theoretical curiosity that was of no practical astrophysical significance. In the last two decades astrophysicists have discovered several new potential sources and have come to believe that it not only may be possible to detect gravitational waves directly but also that their emission may even be the dominant process in the evolution of some astrophysical objects.
GENERATION AND DETECTION
Electromagnetism and gravity are the only two fundamental, longrange forces in nature. Just as accelerated electric charges generate electromagnetic radiation, so do accelerated ``gravitational charges,'' that is, masses, generate gravitational radiation. Simply by analogy with electromagnetism, it is not surprising that gravitational waves are predicted by general relativity and every other viable theory of gravity. Furthermore, if gravity is to obey the laws of Einstein's special theory of relativity, then gravitational radiation must travel at the speed of light.
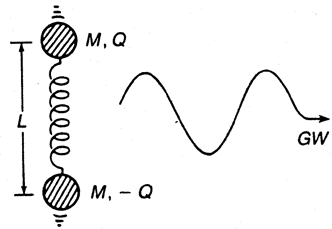
Because all electric charges have mass, one might expect gravitational radiation to be as abundant as electromagnetic radiation; however, this is not the case. Consider the system indicated in Fig. 1 that depicts two particles of the same mass M and opposite electric charge ±Q oscillating at opposite ends of a spring of length L. The ratio of the power PG emitted in gravitational radiation to the power PEM emitted in electromagnetic radiation by this system is
where
Figure 1. Oscillating masses (electric
charges) are a source of gravitational (electromagnetic) waves. This
same system can also absorb energy from an incident gravitational
(electromagnetic) wave.
Electromagnetic radiation is detected by a wide variety of
instruments, all of which operate on the same principle:
electromagnetic waves exert force on electric charges. Likewise,
gravitational radiation can be detected by the force it exerts on
masses. If a GW is incident on the spring system of
Fig. 1 the masses
will be driven into oscillation. The amplitude of the oscillations,
however, is very small, again because of the weakness of gravity. In
fact, the ratio of the energy absorbed from a gravitational wave to
the energy absorbed from an electromagnetic wave of equal strength is
given by exactly the same ratio as in the equation.
Figure 2. Lines of force of a plane,
polarized gravitational wave in the plane perpendicular to the
direction of propagation of the wave. The resultant accelerations of
four test masses, A, B, C, and D are indicated by bold arrows.
As is characteristic of electromagnetic waves, GWs have two possible
polarizations and exert force on matter only in directions
perpendicular to the direction of propagation of the wave. The energy
in the wave decreases inversely with the square of the distance from
the source. For a polarized GW the lines of force in the plane
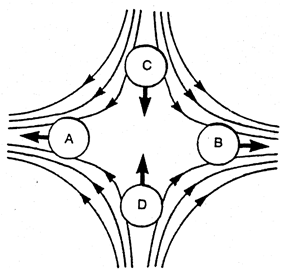
perpendicular to the direction of propagation are illustrated in
Fig. 2. The resultant accelerations of four test
masses, A, B, C, and
D, are indicated by arrows. One-half cycle later the directions of the
lines of force and accelerations are reversed. A representation of the
other possible polarization is obtained by rotating the figure by
45°. The primitive gravitational wave detector of
Fig. 1 is obtained
by simply connecting masses A and B (or C and
D) by a spring.
Considering the inherent weakness of gravity, laboratory sources of
gravitational radiation are nonexistent. For example, a 1-ton steel
bar spun so rapidly that it is on the verge of being ripped apart by
centrifugal force radiates less than 10-30 W. (This problem was
considered by Einstein in 1918.) By contrast, existing detectors are
only sensitive enough to detect such a source (at a distance of one
wavelength) if it emits more than 106 W. Current hopes for directly
detecting GWs are pinned on astrophysical sources in which massive
bodies undergo tremendous accelerations. Short term binary star
systems emit strongly (1025-1029 W) at frequencies
from 10-4-10-3 mHz,
but there are currently no detectors capable of detecting such sources
even nearby. Even though not directly detectable, the energy loss from
the short term binary pulsar PSR 1913+16 due to gravitational
radiation has been measured by precise timing observations of the
pulsar orbit. These measurements agree with the predictions of
general relativity to within 1%, a result which is an important
confirmation of the existence of GWs. A much stronger source is
gravitational collapse to a black hole during which a large fraction
of the mass of an entire star may be accelerated to velocities
approaching the speed of light. It is expected that as much as
1049 W
of GWs will be emitted from such a source in the form of a pulse of
duration 0.001 s. It has also been conjectured that massive black
holes (105-109 M
The first attempts to detect gravitational waves were made in the
1960s by Joseph Weber who acoustically suspended a massive (1400-kg)
aluminum cylinder and monitored the level of excitation of its lowest
vibrational mode. Resonant at 1660 Hz, this detector was designed to
be sensitive to the burst of gravitational radiation predicted to
accompany the formation of a solar mass black hole. His 1969 claim of
detection of GWs was not confirmed and it is now the consensus of
opinion within the scientific community that GWs have not yet been
directly observed. Several cryogenically cooled cylinders are now in
operation with a sensitivity adequate to detect the GWs emitted from
gravitational collapse occurring anywhere in the Milky Way
galaxy. None has been detected. Laser interferometers that detect the
relative displacement of two mirrors (separated by hundreds of meters)
of a Michelson interferometer are potentially more sensitive detectors
that respond to a wider range of frequencies. It is hoped that several
of these instruments will be in operation in the 1990s with a
sensitivity sufficient to detect gravitational collapse in galaxies
outside our own. At lower frequencies (10-3 Hz), radar ranging of
spacecraft and the monitoring of solid Earth vibrations have been
employed but these methods are not yet sensitive enough to detect such
events as the formation of massive black holes in distant
galaxies. The effect of GWs on the arrival times of pulsars has been
used to place upper limits on a background of GWs with periods of a
few years. These limits already have provided important constraints on
some models of cosmic strings.
The observations of the binary pulsar PSR 1913+16 have established the
existence of gravitational radiation, but as an astrophysical source
of GWs this system is the least interesting object imaginable, that
is, two point particles in orbit around one another. The main
motivation of researchers in the field is not simply to observe GWs
directly and thereby confirm their existence, but rather to be able to
use them to probe deeply into the regions of strong gravitational
fields and dense matter that may block other forms of radiation. Only
when GWs are detected from one or more of the spectacular
astrophysical phenomena mentioned above will gravitational wave
astronomy be considered a legitimate branch of astrophysics.
L /
)2
is the wavelength
of the radiation. If the particles are
electrons (which are responsible for most of the electromagnetic
radiation we observe), the first factor alone is 10-43, which
illustrates the incredible weakness of gravity. The second term in the
preceding equation is proportional to the square of the ratio of the
speed of the masses to the speed of light and is always less than
1. From this example it is clear that large, rapidly moving masses are
the best sources of GWs.
SOURCES
) are located in the nuclei
of many galaxies and
quasars. During their formation these objects could emit as much as
1054 J of energy in the form of GWs at frequencies between
10-1 and
10-5 Hz. Several more exotic sources of low frequency gravitational
radiation have been suggested, for example, quantum gravity
fluctuations in the early universe, a quantum chromodynamic phase
transition from free quarks into nucleons and oscillating cosmic
strings. The period of GWs from these sources range from days to years
and are out of the range of laboratory detectors.
DETECTORS
GRAVITATIONAL WAVE ASTRONOMY
Boughn, S.P. (1979). Detecting gravitational waves.
American Scientist 68 174.
Davies, P.C.W.
(1980). The Search for Gravity Waves.
Cambridge University Press, Cambridge.
Jeffries, A.D., Saulson, P.R., Spero, R.E., and Zucker, M.E.
(1987). Gravitational wave observatories.
Scientific American 256 (No. 6) 50.
Misner, C.W., Thorne, K.S., and Wheeler, J.A.
(1973). Gravitation. W.H. Freeman, San Francisco.
Weisberg, J.M., Taylor, J.H., and Fowler, L.A. (1981).
Gravitational waves from an orbiting pulsar.
Scientific American 245 (No. 4) 74.
See also Black Holes, Theory; Cosmology, Cosmic Strings;
Gravitational Theories; Pulsars, Binary; Pulsars, Millisecond; Stars,Neutron, Physical Properties and Models.