COSMOLOGY, INFLATIONARY UNIVERSE
Robert H. Brandenberger
The inflationary universe is a cosmological model in which there is a period during the very early universe when the volume of space expands exponentially. A period of inflation may arise when matter is described by particle physics (instead of by an ideal gas) in the early universe. Inflationary models provide potential solutions to some of the problems of standard cosmological models. They also provide a mechanism which produces energy density fluctuations which can seed galaxies and other structures in the universe.
MODELS
The inflationary universe may arise when one couples particle physics and classical general relativity, in particular when one describes matter in terms of fields. It is known that field theory describes the interaction of particles very well at high energies and temperatures when the ideal gas description of matter breaks down. Hence, the cosmological models obtained in this way will give a better description of the early universe than the classical models.
When describing matter in terms of fields, it is possible to obtain
equations of state with negative pressure. For a scalar field (a field
which does not change under Lorentz transformations)  (x, t), three
terms contribute to the energy density
(x, t), three
terms contribute to the energy density  and pressure p
- the kinetic
energy density, the spatial gradient energy, and the contribution of a
potential energy term V(
and pressure p
- the kinetic
energy density, the spatial gradient energy, and the contribution of a
potential energy term V( ):
):
Here, R (t) is the scale factor of the universe. If
In some models,
Models with -
Scaler fields arise in many particle physics models. They are often
used to break gauge symmetries. In this case, a potential of the form
of curve (a) in Fig. 1 is required. New
inflationary universe models
take such a potential and assume that at very early times
Figure 1. A sketch of the potential
V(
Constraints stemming from the magnitude of density perturbations
produced during inflation requires the coupling constant which
determines the flatness of V(
Inflationary models provide a potential explanation of the flatness
of the universe and of its homogeneity on large scales. Homogeneity
follows from the observed isotropy of the microwave background
radiation to less than 1 part in 104. The flatness can be quantified
by comparing the present energy density
In classical cosmology, the isotropy of the microwave background has
no causal explanation, because the radiation detected in different
directions on the sky comes from patches of the last scattering
surface, which at last scattering trec could not have
been in causal
contact. Similarly, in classical cosmology
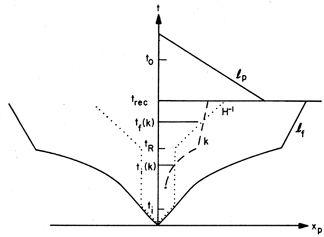
As illustrated in Figure 2, in inflationary
models the horizon
expands exponentially during the period of inflation. Provided
inflation lasts for more than a few Hubble expansion times
H-1 (t),
the horizon at teq is larger than the surface at
trec from which the microwave radiation reaches us.
Similarly, inflation solves the flatness problem. During the period
of inflation, |
Inflationary models provide a possible mechanism for generating the
primordial density perturbations which can lead to structure
formation. The simplest inflationary models give a scale invariant
spectrum of linear, adiabatic random phase perturbations. Scale
invariant means that the root-mean-square mass perturbation on a fixed
comoving scale has a value which is independent of the scale when
measured at the time when the scale equals the Hubble radius.
The basic mechanism is illustrated in
Figure 2. All comoving scales
originate inside the Hubble radius (causal horizon) during the de
Sitter phase. Hence, it is possible to obtain a causal explanation of
the origin of perturbations.
Quantum fluctuations in the de Sitter phase which arise on all
comoving scales are frozen in as classical perturbations on scale k
when the wavelength k-1 equals the Hubble radius at
time ti (k).
Between ti (k) and tf (k), the time
when the wavelength ``reenters'' the
Hubble radius, the mass perturbations grow according to linear
gravitational perturbation theory and increase by a constant
factor. Since the amplitude of the perturbations is k independent at
ti (k), a scale-invariant spectrum is generated.
The amplitude of the spectrum of density perturbations depends on
the coupling constants in the particle physics model. In order not to
give a too-large amplitude, sell-coupling constants in V(
The inflationary universe has become a paradigm in search of a
concrete realization. There have been attempts to obtain inflation in
supergravity and superstring models, in theories with modified gravity
or with extra dimensions. Extended inflation is a new attempt to use a
dynamical Brans-Dicke scalar field to obtain generalized inflation.
Chaotic inflation is at present the most developed model. It
predicts that on scales much larger than our present horizon, the
universe will consist of many very different, almost disconnected
miniuniverses.
In models in which more than one scalar field is important during
the period of exponential expansion, it is possible to obtain
deviations from scale invariance, isothermal perturbations, and even
non-Gaussian fluctuations.
 = 1/2
= 1/2  2 + 1/2
R-2 (t) (
2 + 1/2
R-2 (t) (
 )2 +
V(
)2 +
V( ),
),
 2 - 1/6 R-2 (t)
(
2 - 1/6 R-2 (t)
(
 )2 - V(
)2 - V( ).
).
 (x, t) is
homogeneous and static and V(
(x, t) is
homogeneous and static and V( ) is positive, the equation of state is
p = -
) is positive, the equation of state is
p = -  . Hence, using the Einstein equations for a Friedmann
universe, one obtains exponential increase of the scale factor (the de Sitter
phase).
. Hence, using the Einstein equations for a Friedmann
universe, one obtains exponential increase of the scale factor (the de Sitter
phase).
 is homogeneous
but time dependent. In this case,
the equation of state is no longer p = -
is homogeneous
but time dependent. In this case,
the equation of state is no longer p = - . However, it is still
possible for such a cosmological model to solve the homogeneity and
flatness problem (see the following), provided p < -1/3
. However, it is still
possible for such a cosmological model to solve the homogeneity and
flatness problem (see the following), provided p < -1/3  . This is the
condition for R (t) to increase more rapidly than the Hubble radius
H-1 (t), where
. This is the
condition for R (t) to increase more rapidly than the Hubble radius
H-1 (t), where
 (t) / R (t)
(t) / R (t)
 <
p < -1/3
<
p < -1/3  are
said to give rise to to give rise to generalized inflation.
are
said to give rise to to give rise to generalized inflation.
 (x)
(x)  0.
0.  (x)
will slowly roll towards one of
the of the minimum energy values ±
(x)
will slowly roll towards one of
the of the minimum energy values ± . If the potential is very flat,
then it will take the field a long time to reach ±
. If the potential is very flat,
then it will take the field a long time to reach ± . During most of
the rolling phase, p
. During most of
the rolling phase, p  -
- and
the universe expands exponentially.
and
the universe expands exponentially.
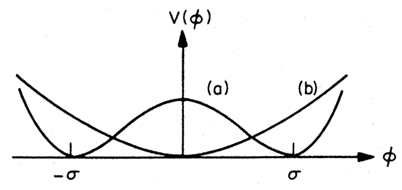
 ) postulated in new
inflationary universe models (a) and for chaotic inflation (b).
) postulated in new
inflationary universe models (a) and for chaotic inflation (b).
 ) to be so small that the initial
condition
) to be so small that the initial
condition  (x)
(x)  0 can no longer be
justified. This is taken into account
in the chaotic inflationary universe. In this case, either potential
(curve a or b of Fig. 1) can be
chosen. The part of the universe inside
our horizon is assumed to stem from a region in space where initially
0 can no longer be
justified. This is taken into account
in the chaotic inflationary universe. In this case, either potential
(curve a or b of Fig. 1) can be
chosen. The part of the universe inside
our horizon is assumed to stem from a region in space where initially
 (x) was homogeneous over
a few Hubble volumes and in addition
(x) was homogeneous over
a few Hubble volumes and in addition  >> mpl
(where mpl stands for the Planck mass). In this case,
>> mpl
(where mpl stands for the Planck mass). In this case,
 (x) will slowly
roll towards
(x) will slowly
roll towards  =
=  (or
(or  = 0 in the case of curve b in
Fig. 1), its motion
being damped by the expansion of the universe. Again, p
= 0 in the case of curve b in
Fig. 1), its motion
being damped by the expansion of the universe. Again, p  -
-  and
inflation occurs.
and
inflation occurs.
HOMOGENEITY AND FLATNESS PROBLEMS
 with the energy density
with the energy density  c
for a flat (K = 0)
universe. The ratio
c
for a flat (K = 0)
universe. The ratio  =
=  /
/  c is most
likely between 0.1 and 1.
c is most
likely between 0.1 and 1.
 = 1 is an unstable fixed
point of an expanding universe. Thus, having
= 1 is an unstable fixed
point of an expanding universe. Thus, having  close to 1 today
implies that
close to 1 today
implies that  had to be
tuned to almost
had to be
tuned to almost  = 1 with an
extreme accuracy at early times.
= 1 with an
extreme accuracy at early times.
 - 1|
decreases exponentially. Thus,
- 1|
decreases exponentially. Thus,  in the range
between 0.1 and 1 today no longer requires unnatural fine tuning in
the very early universe.
in the range
between 0.1 and 1 today no longer requires unnatural fine tuning in
the very early universe.
INFLATION AND DENSITY PERTURBATIONS
 ) typically
must be tuned to be smaller than 10-12. This is a serious
problem which affects most inflationary models.
) typically
must be tuned to be smaller than 10-12. This is a serious
problem which affects most inflationary models.
RECENT RESULTS
Guth, A. and Steinhardt, F. (1984). The inflationary universe.
Scientific American 250 (No.5) 116.
Linde, A. (1984). The inflationary universe. Rep. Prog. Phys.
47 925.
Linde, A. (1987). Particle physics and inflationary cosmology.
Physics Today 40 61.
Linde, A. (1990). Inflation and Quantum Cosmology. Academic
Press, Boston.
Turner, M. (1985). The inflationary paradigm. In Proceedings of
the Cargese School on Fundamental Physics and Cosmology,
J. Audouze and J.Tran Thanh Van, eds. Editions Frontieres,
Gif-sur-Yvette.
See also Background Radiation, Microwave; Cosmology,
Observational Tests; Cosmology, Theories.