GALAXIES, SPIRAL, NATURE OF SPIRAL ARMS
Ray Carlberg
The beautiful spiral patterns that occur in disk galaxies are now understood to be primarily a result of gravitational forces between stars and gas in a shearing, rotating disk. The path toward this simple idea has had many twists, turns, and blind alleys.
Two previous, incorrect theories are that spirals are galactic analogues of a spinning garden sprinkler spraying from the ends of a rotating central object or that magnetic fields trap the gas so that the two are wound up together in spiral patterns.
Attempts to understand spiral structure on the basis of gravitational forces between very large numbers of stars have a long history, but limited success precisely because there are so many stars in galaxies. In fact, there are so many stars in galaxies that any single star in a galaxy could be removed and the motion of every other star would be almost the same, which is very different from the situation in star clusters. This feature has the important consequence that the motions of stars in galaxies are controlled by the collective gravity of all the stars, and do not depend on the details of any star's position. This type of system, called a collisionless fluid, allows one to ignore the details of the individual stars, but requires complex techniques of analysis for adding together the joint motions and gravitational effects of all the stars.
The fact that stars cannot interact as individuals immediately leads to a simple explanation of the fact that all spirals appear to be ``trailing,'' that is, they lag the direction of rotation with increasing radius in the disk. The explanation is that gravitating systems attempt to increase their gravitational energy, or at least become more concentrated, if at all possible. For a disk of stars an increase in gravitational energy of the central region can only occur if the stars move closer to the center. To move stars inward requires that they lose angular momentum, which can be accomplished if there is a torque directed opposite to their direction of rotation. A trailing spiral pattern supplies just such a torque because the stars in the spiral wave near the center are pulled backward by the stars further out in the spiral. Consequently the central gravitational energy is increased at the expense of a decrease in the energy of stars further out in the disk.
The density wave theory introduced by Chia-Chiao Lin and Frank H. Shu began the modern era of understanding spirals in terms of gravitational dynamics. Using a simplified set of equations they showed that the solutions were waves that maintained their spiral shape, rotating through the stars and gas in a galactic disk. In the inner part of the disk the stars move faster than the spiral and overtake it; in the outer part of the disk the spiral pattern moves faster than the stars and the relative velocities are reversed. For the gas clouds in the disk this idea predicts that they will be compressed and form dark dust lanes on the inside of the trailing spiral patterns, as is usually the case. More recently detailed investigations of the relative locations of the spiral arms as seen in the stars as compared to the arms seen in the molecular gas provide additional evidence that spiral arms are waves that move through the gas and stars in the disk.
The simple version of the density wave theory requires that the same pattern rotates around and around for the lifetime of the galaxy. However, analysis shows that only in special situations can these density waves persist. The more likely result is that the inner part of the wave travels toward the center, the outer part travels outward, and, in the absence of a source of new waves, the spiral arm dies away. Resolving the question ``Where do spiral arms come from?'' remains an issue of current investigation.
Real galaxies provide only a limited amount of information about spiral waves. The main problem is that a typical galaxy has a rotation period of 100 million years, so we cannot simply observe the galaxy to see whether the wave pattern remains steady or dies away. Computer simulations have done much to alleviate this problem. Although the equations of motion for stars in a disk were written down by Isaac Newton, it is not simple to solve them for a system of billions of stars. Therefore, computer studies usually have tried to mimic several thousand stars with the motion of one ``superstar.'' If the superstar becomes too massive then the studies start seeing the motions of other stars as individuals, rather than the collective effect of the collisionless fluid that is an essential feature of disk galaxies. For these reasons, it is only recently that computer simulations have been large enough and accurate enough to provide a lot of valuable information regarding the motions of stars and gas within a galaxy disk.
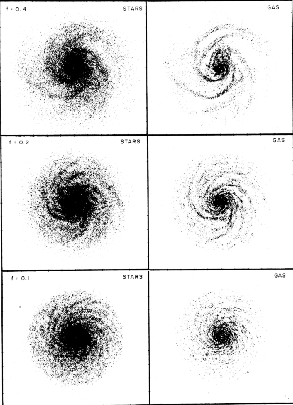
The results of one simulation incorporating 30,000 superstars and 10,000 super gas clouds are shown in Fig. 1. It is immediately obvious that these model galaxies have strong resemblances to real galaxies: the spirals are relatively open, the top one is nearly bisymmetric but not quite, and it is possible to produce model galaxies with many, very fine, spiral arms. It is also quite easy to make the barred spirals that are the other part of Edwin Hubble's tuning fork diagram of galaxy classification.
Part of the process that is responsible for the spirals in these model galaxies is quite well understood. In the models a gradual inward drift of stars in the central region can be detected exactly as predicted by the idea that explains trailing spirals. However, measurements of the motions of the spirals in these galaxies find that the patterns are not permanent: they come and go, but at almost any time spirals of the same general appearance are present.
A good partial understanding of these transient spiral patterns was developed prior to the computer models, and the process has been dubbed swing amplification. The same effect that makes a trailing spiral wind inward and disappear does exactly the opposite to leading spiral waves. A small leading spiral will travel outward and grow enormously, by factors of up to a hundred in intensity, into a strong training pattern. That is, spirals do not preserve their shape, but are bent backward by the rotation of the disk although not nearly as fast as the motion of the stars alone gives. The spirals continue to move through the stars, thus preserving the ability to predict the characteristics of the dust lanes. However, once a very large trailing spiral has been created it then continues to slowly wind up and fade away. Careful measurements of a large number of simulations confirm that this idea explains many of the details of the changes in the spiral features in these simulations and can nicely explain the trend of increasing number of spiral arms seen in the diagram.
The keys to understanding the amplification is the rotation of the disk and the idea of pumping a swing. To increase the amplitude of motion on a garden swing, it is crucial that the pushes be applied at the correct times, say at both the forward and backward ends of the swing. Such a tuning of an applied force to an oscillator is known as a resonance. In a galaxy the situation is a little more complicated than a swing. Stars do not travel around the disk in perfect circles, but orbit on precessing ellipses that can be conveniently thought of as the combination of motion around a circle combined with a small ``epicycle'' (as in the Ptolemaic theory of the solar system). Stars on orbits nearer the center go around the circle (not the epicycle) in a shorter time than those further out, an effect that will destroy any material feature within the disk of stars. The epicycles themselves generally have longer periods with increasing radius in the disk. However, it turns out that for the mass distributions of most galaxies the combination of the motion around the circle and half of the epicyclic frequency does not vary much with radius. That is, if a two-armed spiral pattern is created with a pattern speed that matches this combination of frequencies, than the stars on their slightly elliptical orbits will be able to respond in tune with this oscillation; that is, a wide range of radii will be near a resonance of the applied spiral wave so that it should grow in intensity. Ordinarily this spiral wave amplifier does not have a ``feedback'' circuit available, so the wave is excited, grows into the large visible spiral, and then fades away as the shearing forces overwhelm the amplifying forces.
A question only partially answered is ``Where do the leading spirals that trigger the whole process originate?'' Within the computer models the answer is fairly readily evident because these models contain 10,000 gas clouds, similar to the number in real galaxies. Quite frequently these clouds are positioned in such a way that chance alignments effectively create leading spiral patterns. Furthermore, the remnants of previous trailing spirals as they wind up leave small gaps and debris from spiral arms that can by chance line up to create a small leading spiral that keeps the process continually recurring. This continually recurring process can be damped down since the spirals disturb the star orbits, causing them to become less circular and therefore less easy to organize into spiral patterns. However, as long as the galaxy has a supply of young stars and gas in which the spirals form, the spirals can keep recurring.
In the end a complete theoretical description of all the details of spiral patterns will involve a tremendous amount of complicated physics of stars, gas, magnetic fields, and gravity. A very good approximate description of spiral structures is a description of many stars moving about as described by Newton's dynamics and theory of gravity. Stars moving together in nearly circular orbits are strong amplifiers of regions of higher star density, and they create the visible trailing spirals that we observe.
-
Bertin, G. (1980). On the density wave theory for normal spiral
galaxies. Phys. Rep. 61 1.
Carlberg, R. and Freedman, W. (1985). Dissipative models of spiral
galaxies. Astrophys. J. 298 486.
Hohl, F. (1971). Numerical experiments with a disk of stars.
Astrophys. J. 168 343.
Lin, C.C. and Shu, F.H. (1964). On the spiral structure of disk
galaxies. Astrophys. J. 140 646.
Toomre, A. (1977). Theories of spiral structure.
Ann. Rev. Astron. Astrophys. 15 437.
Toomre, A. (1981). What amplifies the spirals? In The Structure
and Evolution of Normal Galaxies, S.M. Fall and D. Lynden-Bell,
eds. Cambridge University Press, Cambridge, p. 111.
See also Galactic Structure, Spiral, Interstellar Gas, Theory;
Galaxies, Spiral, Structure.