previous

COSMOLOGY, POPULATION III

Bernard J. Carr

The term ``Population III'' has been used to describe two types of stars: (1) the ones which form out of the pristine gas left over after cosmological nucleosynthesis and generate the first metals; and (2) the ones which have been hypothesized to provide the dark matter in galactic halos. Stars of the first kind definitely exist, but may not warrant a special name. Those of the second kind may not exist, because galactic halos could also be composed of some sort of elementary particle, but they certainly warrant a special name if they do, and they could have many interesting cosmological consequences. Population III stars of either kind could be pregalactic, but they might also have formed during the first phase of galaxy formation.

FORMATION OF POPULATION III STARS

In the most conservative cosmological scenario, the first stars form in the process of galaxy formation: As each protogalaxy cools and collapses, it fragments first into a spheroidal distribution of Population II stars, and then - if there is any gas left over - into a rotationally supported disk of Population I stars. The problem with this picture is that, in both of the standard scenarios for the origin of cosmological structure, the first bound objects would be much smaller than galaxies. For example, in the hierarchical clustering scenario the first bound clouds have a mass of about 106 Msmsun and bind at a redshift of order 100. Larger bound objects - like galaxies and clusters of galaxies - would then build up through a process of gravitational clustering. A currently popular version of this model is the ``cold dark matter matter'' scenario, in which the density of the universe is dominated by some cold elementary particle like the photino or axion. In the pancake scenario, the first objects to appear are of cluster or supercluster scale and they form at a rather low redshift. This applies, for example, in the ``hot dark matter'' picture, in which the universe's mass is dominated by hot particles like neutrinos with nonzero rest mass. However, one still expects these pancakes to fragment into clouds of mass 108 Msmsun and these clouds must then cluster in order to form galaxies. In both scenarios, therefore, an appreciable fraction of the universe must go into subgalactic clouds before galaxies themselves form.

The question then arises of what happens to these clouds. In some circumstances, one expects them to be disrupted by collisions with other clouds because their cooling time is too long for them to collapse before coalescing. However, there is usually some subgalactic mass range in which the clouds survive. In this case, they could face various possible fates. They might just fragment into ordinary stars and form objects like globular clusters. On the other hand, the conditions of star formation could have been very different at early times and several alternatives have been suggested.

  1. The first stars could have been smaller than at present because of the enhanced formation of molecular hydrogen at early epochs.

  2. They could have been larger than at present because the lack of metals or the effects of the microwave background would increase the fragment mass.

  3. There may have been a mixture of small and large stars; for example, angular momentum effects could lead to a disk of small stars around a central very massive star, or massive stars could form in the core of the cloud and low-mass stars in the outer regions.

  4. The first clouds may not fragment at all, but might collapse directly to supermassive black holes or remain in purely gaseous form and become Lyman-alphaclouds.

This indicates that, although there is clearly considerable uncertainty as to the fate of the first clouds, they could well fragment into stars that are very different from the ones forming today. They certainly need to be very different if they are to produce much dark matter. Note that the appellation Population III is sometimes assigned to the first clouds rather than the first stars. However, in this case, all the stars which they spawn must also be called Population III, and this can lead to semantic confusion if the clouds fragment bimodally. It is therefore more sensible to reserve the term Population III for the stars.

It is not necessarily required that Population III stars be pregalactic. Some of the arguments for their having a different initial mass function (IMF) would also apply if they formed protogalactically, and this gives rise to a less radical hypothesis, in which the Population III objects form during the first phases of protogalactic collapse. In this case, the Population III stars or their remnants would be confined to galaxies, whereas they would be spread throughout space in the pregalactic case.

POPULATION III AS THE FIRST METAL PRODUCERS

Since heavy elements can only be generated through stellar nucleosynthesis, the existence of stars of type (1) is inevitable. However, the stars warrant a special name only if they are qualitatively different from ordinary Population II stars. For example, it would not be justified if the first metal-producing stars were merely the ones at the high-mass end of the Population II mass spectrum. For in this case they would generate the first metals simply because they evolve fastest. The introduction of a new term would only be warranted if the first metal-producing stars formed at a distinct epoch or if the IMF of the first stars was bimodal (i.e., with a distinct population of high-and low-mass stars forming in different locations).

If one studies the abundances of metal-poor stars in our own galaxy, there is no compelling reason for supposing the first stars were distinct from Population II. For example, field halo stars with Z < 0.1 Zsmsun have enhancements in the ratios of O, Mg Si, and Ca to Fe by a factor of 3 relative to the Sun, but this is naturally explained by the fact that these elements are preferentially produced by the sort of massive stars which would complete their evolution on the time scale (108 yr) associated with the formation of the galactic halo. Thus, abundance data itself does not require the existence of Population III stars.

The best evidence for a distinct population of stars would be a lower cutoff in the metallicity distribution of Population II stars. If the first stars had the same IMF as today, with a lower cutoff at about 0.1 Msmsun, one might expect stars smaller than 0.8 Msmsun (whose lifetime exceeds the age of the Universe) to display arbitrarily low metallicity. At one time, it seemed there was a metallicity Zmin of order 10-5 below which no stars were found. If this were true, it would suggest that the first stars had an IMF with a lower cutoff above 0.8 Msmsun. For only then could they produce the minimum enrichment Zmin without surviving until the present epoch. This would imply that the first stars had a different IMF from ordinary Population II stars. Unfortunately, the evidence for such a cutoff is now in dispute: The Z distribution for Population II stars extends well below 10-5 and there exists one object with Z = 6 x 10-7. In any case, the number of low-Z objects is not necessarily incompatible with the assumption that the IMF has always been the same; so the first stars may not have been qualitatively different from Population II stars. Thus the introduction of the term Population III may be unnecessary in this context.

POPULATION III AS DARKMATTER PRODUCERS

The success of the standard Big Bang picture in explaining the light element abundances only applies if the baryon density is about 10% of the critical density. Since the theory of inflation requires the total density to have the critical value, this suggests that there must be much nonbaryonic dark matter (most of it unclustered). On the other hand, visible material only has about 1% of the critical density, so it seems that there must also be some baryonic dark matter. It is possible that this is in the form of a hot intergalactic medium, but there could also be enough of it to explain the dark matter in galactic halos. The dark baryons in halos cannot be in the form of ordinary gas, or else they would generate too may x-rays. They must therefore have been processed into some dark form through a first generation of pregalactic or protogalactic stars.

In principle, there are many mass ranges in which stars could produce dark remnants. For example, stars smaller than 0.1 Msmsun would always be dim enough to explain galactic halos and those smaller than 0.08 Msmsun (jupiters; also called brown dwarfs) would never even ignite their nuclear fuel. Stars in the range 0.8-4 Msmsun would leave white dwarf remnants, whereas those between 8 Msmsun and some mass MBH (probably about 50 Msmsun) would leave neutron star remnants. In either case, the remnants would eventually cool and become dark. Stars more massive than MBH would leave black holes. The ones larger than 100 Msmsun are termed very massive objects (VMOs), and are particularly interesting because they could collapse entirely (without any metal ejection) due to an instability encountered in their oxygen-burning phase. This would apply for VMOs larger than Mc approx 200 Msmsun. Stars larger than 105 Msmsun are termed supermassive objects (SMOs), and would collapse directly to black holes due to relativistic instabilities even before nuclear burning, at least if they were metal-free. It must be stressed that the existence of VMOs and SMOs is entirely speculative and they are invoked primarily for the purpose of making dark matter.

Although stars can in principle produce dark remnants, various constraints require that the dark matter in galactic halos can only be baryonic if it comprises jupiters or the black hole remnants of VMOs. These constraints are summarized in Fig. 1. Low-mass stars are excluded by source count limits, other stellar remnants by nucleosynthesis and background light constraints, and supermassive black holes by dynamical considerations. At first sight, it might seem rather unlikely that Population III clouds would fragment into such objects with high efficiency, but we have seen that there are theoretical reasons for expecting the first stars to be larger or smaller than at present.

Figure 1

Figure 1. Constraints on the density of Population III stars of mass M. Omega* is the density in units of the critical cosmological value; Omega* = 0.1 corresponds to the density associated with galactic halos. The shaded region is excluded, the light constraint depending on the redshift (z) at which the stars burn.

In fact, there are circumstances where dark stars form profusely even at the present epoch. Direct observational evidence that gas can be turned into low-mass stars with high efficiency may come from x-ray observations of cooling flows in the cores of rich clusters. These suggest that 90% of the gas is being turned dark, possibly as a result of the high pressure. Since such cooling flows are confined to the central galaxies in clusters, they could not explain the dark matter in galactic halos. However, one could expect analogous high-pressure flows to occur at earlier cosmological epochs, and these would have been on much smaller scales than clusters. This conclusion pertains in either the hierarchical clustering or pancake scenarios. One could envisage forming dark clusters of jupiters which then agglomerate to form galactic halos. Although VMOs are certainly rare at the present epoch, massive stars do seem to form efficiently in starburst galaxies, and they may have been more abundant in the past. VMOs would certainly have had more exciting cosmological consequences than jupiters.

Note that the formation epoch is very important for the relative distribution of baryonic and nonbaryonic dark matter. If Population III stars form before galaxies, one might expect their remnants to be distributed throughout the universe, with the ratio of the baryonic and nonbaryonic densities being the same everywhere. If they form at the same time as galaxies, one would expect the remnants to be confined to halos with the baryonic component probably dominating.

WHAT POPULATION III STARS CAN EXPLAIN

In this section we will discuss some of the cosmological consequences of Population III stars. We will mostly focus on the VMO scenario, but the last three effects could be important in a more general context. Although Population III stars can explain certain cosmological problems, it would be stressed that this does not provide unequivocal evidence for their existence, because they are not only explanation. Figure 2 summarizes the effects.

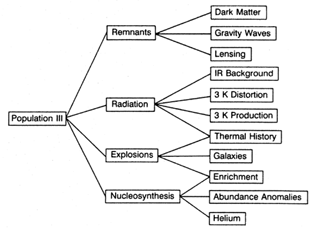
Figure 2

Figure 2. Cosmological consequences of Population III stars.

Infrared Background The most direct evidence for a population of VMOs would come from the detection of the background light they generate. Each VMO has the Eddington luminosity and a mass-independent surface temperature of about 105 K. In the absence of dust absorption, one would expect a background peaking in the infrared with a density of order 10% that of the microwave background. The detection of such a background has in fact been reported at around 2 µm, although this has not yet been verified. In any case, comparison with the upper limits on the background radiation density in the IR band shows that VMOs with the density required to explain galactic halos would have to burn at a redshift exceeding 30 - at least in the absence of dust - and this would imply that they were necessarily pregalactic.

Microwave Distortions If dust were present, the radiation from VMOs would be reprocessed into the far-infrared or submillimeter range, where the limits on the background density are weaker. In the latter case, the radiation would merely appear as a distortion of the microwave background. The dust could either be confined to galaxies (if they cover the sky), or it could be pregalactic in origin. There have, in fact, been two claimed detections of such a back-ground. Data from the Infrared Astronomical Satellite (IRAS) may indicate a background at 100 µm with 10% of the microwave density, although this may be due to zodiacal emission. More recently, a significant distortion in the spectrum of the microwave background radiation has been reported in the 400-700 µm wave-band (cf. the microwave background peak at 1400 µm). This follows a rocket experiment by a team from Nagoya and Berkeley. It corresponds to a submillimeter excess similar to that expected in the VMO-plus-dust scenario. However, preliminary results from the Cosmic Background Explorer (COBE) satellite have not confirmed either the 100-µm or the 400-700-µm excess.

Generation of 3-K Background Some people have proposed that the entire microwave background is dust-grain-thermalized starlight. This is possible in principle, but the grains would have to form at very high redshift (z > 100) or be very elongated in order to thermalize at long wavelengths. An alternative scheme is to propose that the black hole remnants of the stars generate the 3-K background through accretion. Of course, any scheme which envisages the background deriving from Population III stars or their remnants must also require that the early universe was cold or tepid (with the primordial photon-to-baryon ratio being much less than its present value of 109). Stars would, in fact, naturally generate a ratio of order 109. However, it is now more popular to assume that the ratio arises as a result of baryosynthesis in the very early universe.

Helium Production Because pulsations lead to mass-shedding of material convected from its core, a VMO is expected to return helium to the background medium during core-hydrogen burning. The net yield depends sensitively on the mass loss fraction. The yield will be low if the mass loss is very large or very small, but it is optimized if the envelope is ejected during hydrogen-shell burning. In this case, the fraction of mass returned as new helium is DeltaY = 0.25(1 - Yi)2 (1 - Yi / 2)-1, where Yi is the initial (primordial) helium abundance. This would have profound cosmological implications. If Yi = 0.24, corresponding to the conventional primordial value, DeltaY = 0.16, so helium would be substantially overproduced if much of the universe went into VMOs. In this case, the only remaining black hole candidate for the dark matter would be SMOs in the mass range 105-106 Msmsun. On the other hand, if Yi = 0, corresponding to no primordial production, DeltaY = 0.25, which is tantalizingly close to the standard primordial value. This raises the question of whether the Population III VMOs invoked to produce the dark matter might not also generate the helium which is usually attributed to cosmological nucleosynthesis. It must be stressed, however, that the hot Big Bang model also predicts the observed abundances for deuterium, helium-3, and lithium. Although one can conceive of astrophysical ways of generating these elements in a cold universe, they are somewhat contrived.

Dynamical Effects of Halo Holes The most interesting constraint on the mass of any holes in our own galactic halo is associated with their tendency to puff up the galactic disc. A detailed calculation of this effect suggests that halo holes could actually be responsible for all of the observed disk puffing, providing the halo objects have a mass of 2 x 106 Msmsun. While one cannot definitely identify halo holes as the explanation for disk heating (e.g., spiral density waves might also work), it is interesting that the hole mass required can be specified so precisely. Note that this argument does not require that the halo object be a single hole; even a cluster of smaller holes - or indeed a cluster of jupiters - would suffice. From a theoretical point of view, the halo objects are more likely to be clusters because too many supermas- sive black holes would be dragged into the galactic nucleus by dynamical friction. Clusters would be destroyed by collisions within the galactocentric radius where dynamical friction is operative, providing they had a radius larger than 1 pc. Further evidence that galactic halos comprise objects with mass of order 106 Msmsun may come from gravitational lensing effects. Evidence for the jupiters themselves could come from microlensing.

Gravity Waves from Black Holes The formation of a population of pregalactic black holes would be expected to generate bursts of gravitational radiation. The characteristic period of the waves would be in the range 10-2-10-4 s, depending on the holes' mass and formation redshift. If the holes are numerous enough to make up galactic halos, one would expect the bursts to overlap in time to form a background of waves. This background could be detectable by laser interferometry if the mass is below 102 Msmsun or by the Doppler tracking of interplanetary spacecraft if it is in the range 105-1010 Msmsun. The prospects of detecting the gravitational radiation would be even better if the holes formed in binaries, because one would then get both continuous waves as the binaries spiral inward due to gravitational wave emission and a final burst of waves when the components finally merge. This would increase the amplitude of the waves and extend the spectrum to longer periods. One could also hope to observe the mergers which are occurring in nearby galaxies at the present epoch.

Heavy Element Prodution For some purposes it would be advantageous to have a slight pregalactlc enrichment (e.g., to explain the small grain abundance required to produce alleged distortions in the 3-K spectrum), so the question arises of whether Population III stars could generate just a small amount of metals. A rather plausible way of doing this would be to suppose that the formation of the first metal-producing stars is suspended once enough of them have formed to reionize the universe. This would naturally generate a metallicity of order 10-6. If one also wants dark-matter-producing stars, one must either suppose that they form later or fine-tune the IMF.

Thermal History The light generated by Population III stars could have an important effect on the thermal history of the universe even in the conventional Big Bang scenario. During its main-sequence phase, each star (or cluster of stars) would be surrounded by an H II region. The fraction of the universe in such regions would progressively grow, because of both the increasing number of stars and the increasing size of the individual H II regions; even a small density of Population III stars would soon reionize the whole universe. Such reionization could have important cosmological implications (e.g., in reducing anisotropies in the 3-K background). After the H II regions have merged, the universe would maintain a high degree of ionization until the stars cease burning, and even thereafter if they leave black hole remnants which heat the universe through accretion. It is not clear whether more conventional sources (like quasars) can ionize the intergalactic medium early enough. Pregalactic explosions Stars in the mass range

Pregalactic Explosions Stars in the mass range 4-102 Msmsun should produce explosive energy with an efficiency epsilon = 10-5-10-4; larger ones may explode with comparable efficiency if they eject their envelopes during hydrogen-shell burning. This explosive release could have an important effect on the large-scale structure of the universe. One would expect the shock wave generated by each exploding star (or cluster of stars) to sweep up a shell of gas. Under suitable circumstances, this shell could eventually fragment into more stars. If the new stars themselves explode, one could then initiate a bootstrap process in which the shells grow successively lager until they overlap. This mechanism has been proposed in two contexts: (1) as a means to boost the fraction of the universe being processed through pregalactic stars and (2) as a way of producing the giant voids and filaments, whose existence is indicated by observational data. An upper limit to the final shell size in all circumstances is sqrtepsilon times the current horizon size. This is 60 Mpc for epsilon = 10-4 and a Hubble parameter of 100, which is just about large enough to explain the largest voids.

CONCLUSION

We have seen that one must distinguish between metal producing and dark-matter-producing Population III stars. The first must exist, but only warrant a special name if there is a lower cutoff in the metallicity distribution of Population II stars, and it is not clear that this is the case. The second may not exist, but, if they do, they certainly warrant a separate name. They would have to be either jupiters or black holes. The detection of microwave distortions would favor the black holes option, but the claim that cooling flows make low-mass stars may favor the jupiter option. In principle, both kinds of Population III stars could derive from a single mass spectrum, but that would require the IMF to be finely tuned.

Additional Reading
  1. Ashman K.M. and Carr, B.J. (1988). Pregalactic cooling flows and baryonic dark matter. Mon. Not. R. Astron. Soc. 234 219.
  2. Beers, T.C. Preston, G.W. and Schectman, S.A. (1985). A search for stars of very low metal abundance. Astron J. 90 2089.
  3. Bond H.E. (1981). Where is Population III? Ap. J. 248 606.
  4. Bond J.R. Carr, B.J., and Hogan, C.J. (1986). Spectrum and anisotropy of the cosmic background. Ap. J. 306 428.
  5. Carr, B.J. and Lacey, C.G. (1987). Dark clusters in galactic halos? Ap. J. 316 23.
  6. Carr, B.J., Bond, J.R., and Arnett, W.A. (1984). Cosmological consequences of Population III stars. Ap. J. 277 445.
  7. Cayrel, R. (1986). And if Population III were Population II? Astron. Ap. 168 81.
  8. Fabian, A.C., Nulsen, P.E.J., and Canizares, C.R. (1984). Cooling flows in clusters of galaxies. Nature 310 733.
  9. Hartquist, T.W. and Cameron, A.G.W. (1977). Pregalactic nucleosynthesis. Ap. Space Sci. 48 145.
  10. Kashlinsky, A. and Rees, M.J. (1983). Formation of Population III stars and pregalactic evolution. Mon. Not. R. Astron. Soc. 205 955.
  11. McDowell, J.C. (1986). The light from Population III stars. Mon. Not. R. Astron. Soc. 223 763.
  12. Pagel, B.E.J. (1987). Galactic chemical evolution. In The Galaxy, G. Gilmore and B. Carswell, eds. Reidel, Dordrecht, p. 341.
  13. Rees, M.J. (1978). Origin of pregalactic microwave background. Nature 275 35.
  14. Truran, J.W. (1984). Nucleosynthesis. Ann. Rev. Nucl. Part. Sci. 34 53.
  15. White, S.D.M. and Rees, M.J. (1978). Core condensation in heavy halos: A two-stage theory for galaxy formation and clustering. Mon. Not. R. Astron. Soc. 183 341.
  16. See also Background Radiation, Microwave; Cosmology, Big Bang Theory; Cosmology, Galaxy Formation; Gravitational Radiation.

Previous