Marshall H. Cohen
When compact radio sources are examined on a scale of a milliarcsecond (mas) they frequently are seen to contain moving components. This is described as an internal proper motion µ, which is expressed in milliarcseconds per year. It may be converted to an ``apparent transverse velocity'' v with the formula v = µ D(1 + z), where D is an appropriate distance, z is the redshift, and the factor (1 + z) scales the velocity to the value a comoving observer (i.e., one at rest relative to the source) would measure. When v > c (the velocity of light), the motion is called superluminal when v < c, it is subluminal.
This phenomenon has a tiny angular scale, and very long baseline interferometry (VLBI) at radio wavelengths is the only technique capable of seeing it today. Hints of superluminal motion were seen as early as 1969, two years after the invention of VLBl; but the first definitive measurements were not made until 1971, when two teams, one headed by Irwin Shapiro and the other by Marshall Cohen and Kenneth Kellermann, saw changes in the quasars 3C273 and 3C279. These observations followed by four months the accidental discovery, by Shapiro's group, that those objects had simple double structure. For both sources the separation increased in four months, with v > c.
The velocity v is not limited to c by the special theory of
relativity, because it may be due to phase or retardation effects. The
usual description has two bright spots, one (A) stationary, and the
other (B) moving with velocity 
c at an angle 
to the line of sight.
In unit time B moves a distance c, whereas its transverse distance
from A increases by c sin . But the elapsed time for the observer to
see the beginning and end of this motion is only (1 - cos ) because
the velocity of light is finite. Hence the apparent transverse
velocity is
c sin ) /
(1 - cos )
and v has a maximum value 
c when csc =
= (1 - 2)-1/2. Equation
(1) is a general formula and can apply when B is a ``light echo''
with = 1 as
well as to luminous ``bullets'' with < 1, or to regions
successively excited by a wave. In 1967, Martin Rees used Eq. (1) to
explain rapid flux variations in active nuclei, and at that time he
predicted superluminal motion, four years before it was seen!
A different kinematic model could involve motion that is simulated by independent fluctuations in intensity of a few stationary spots. This explanation, however, is incapable of explaining two key features of the observations: (a) all well-determined motions are expansions, never contractions and (b) in some cases spots have been observed to more than double their separation.
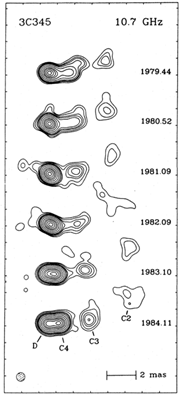
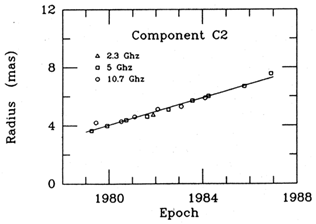
The best-studied source is the quasar 3C345, for which a series of s maps are shown in Figure 1. The increasing separations are apparent, even though these images have lower dynamic range than is becoming available today. Figure 2 shows an ``expansion diagram'' for component C2 of 3C345. The data are well fit by a straight line, indicating a uniform proper motion of 0.47 mas yr-1. With z = 0.595 and q0 = 0.5, standard cosmology gives v = 9.3h-1c, where h = H0 / 100 is the reduced Hubble constant in kilometers per second per 100 megaparsecs.
|
Figure 1. A sequence of maps of 3C 345 made at 10.7 GHz. The smoothing beam is a circular Gaussian of half-width 0.6 milliarcseconds (mas), shown in the lower left corner. [Reproduced from Biretta, Moore, and Cohen (1986) Ap. J. 308, 93.] |
Figures 1 and 2 represent the classic form of superluminal motion. The morphology is characterized by a linear structure with a rather stable, particularly compact, component at one end, and one or more moving components. The end component is called the ``core'' and is thought to be close to the central engine. In one case (3C345), absolute astrometry was able to show that the core is stationary on the sky. A core generally has a flat radio spectrum, whereas the other (moving) components have a steep spectrum. The moving components usually evolve and grow weak at short centimeter wavelengths, with a time scale of 2-10 yr.
|
Figure 2. Expansion diagram for component C2 of 3C 345. The line represents a uniform proper motion of 0.47 mas yr-1. The points, each corresponding to the centroid of C2 at the labeled frequency, cluster tightly about the line, showing that the location of the centroid is nearly independent of frequency. |
A number of other sources have similarly shown this classic behavior, but there are numerous complications.
1. Many sources display more than one traveling component and their speeds may be different. In two well-studied cases (3C273 and 3C345), the more distant components have the higher speeds. In 3C345 the new component C4, born near the core around 1980, was observed to accelerate in 1982.
2. Several sources have stationary components in addition to moving components. The most famous case is 4C39.25, which had been a stable double for a decade. Around 1980, however, a new component appeared near one of the original ones and began traveling superluminally toward the other, which has remained stationary but is fading. None of the three components appears to be a core in the sense described previously, and it is not at all certain that any of the three is truly stationary on the sky.
3. A source with more than two components is usually not straight but shows curvature or even a kink. A major question then has been whether the components move ballistically, on straight lines, or move on curved tracks and perhaps even follow each other like beads on a string. The present indication in both 3C273 and 3C345 is that the motion is along a curved track. In 3C345 the new components C5 and C4 have had curved tracks, but they were at different position angles; that is, they were not like beads on a fixed string. Component C3, however, may be following the track taken earlier by C2. There evidently is a variety of possible motions, and it will take many years of observation to sort them out.
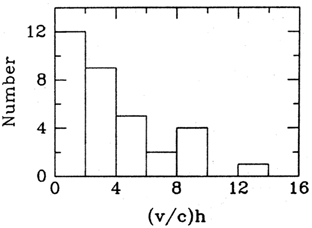
Proper motions (or upper limits) have now been established in about
33 objects, of which 23 are superluminal, 2 are subluminal, and 8 have
upper limits that generally require v <
1.5h-1c. Figure 3 shows the
histogram of their apparent transverse velocities; for those sources
with more than one moving component only the fastest is plotted. The
sample is inhomogeneous and incomplete, but most of the objects were
chosen because they are ``active''; that is, they are variable and
strong, and Fig. 3 is probably representative of
core-dominated
objects. Thus it is significant that the median velocity corresponds
to angle much less than 60°. The median velocity for all objects in
Fig. 3 is 3.3h-1c. From
Eq. (1)the median ``maximum allowed angle''
(for = 1) is
approximately 34h°, which for 0.5 < h < 1 means that most
of the objects are pointed close to our line of sight. Why is there
such a strong selection effect? Three possibilities have been
suggested.
|
Figure 3. Histogram of superluminal velocities for 33 objects. The apparent transverse velocity v is normalized by c, the velocity of light, and is inversely proportional to the reduced Hubble constant h. [Reproduced from Cohen, in BL Lac Objects, Lecture Notes in Physics 334, Springer-Verlag, Berlin (1988) , p. 13.] |
Many Seyfert galaxies are known to have a central torus that blocks optical light and allows a clear view of the central region only from a restricted solid angle around the axis. This idea is geometrically simple, but it is difficult to make it work for superluminal sources, because they are observed at radio wavelengths. Dust is transparent at these wavelengths, and blocking the radiation with plasma requires far more electron density than is customarily ascribed to he narrow-line region.
The moving bright spot must have velocity close to 1; for example,
for for v = 10c, 
0.995. If the radiating material itself is moving
with the same or a similar velocity, then it has a Lorentz factor
10;
that is, it is relativistic. Its radiation is necessarily beamed
into a cone of half-angle -1 rad, and this automatically gives a
strong preference to sources beamed at us. This explanation is usually
favored, because, in addition to explaining the angular anisotropy, it
explains in a simple way the one-sided morphology. Furthermore, it
uses the bulk relativistic motion that appears to be needed in any
event to explain the rapid time variations, the lack of inverse
Compton x-rays, and the polarization asymmetry seen in the large-scale
jets.
Statistical difficulties associated with the thin-beam model have prompted speculation of multiple beams in wide cones. If a source has many narrow beams, all within a wide cone, then there could be a substantial probability that a source oriented at random still has one of its beams aimed close to our line of sight. We would see the Doppler-boosted radiation from that beam but not from the others, and the superluminal jet would look thin when projected on the sky. The beams do not have to coexist like multiple searchlights, but could follow each other; for example, they could be successive shock waves with different trajectories. A general objection to this picture is that in some cases our line of sight should be inside the cone, and then the superluminal motions should be projected into many directions. The source should have a two-dimensional appearance, whereas these sources always have a linear appearance. In support of the wide-cone hypothesis, however, is the observation that the two new components in 3C345 emerged from the core at rather different position angles, and have been following different tracks.
The synchrotron radiation from a beam with bulk relativistic motion
has an angular pattern given by 
n, where n 
(2 - 
), is the spectral
index of the radiation, and
is the Doppler factor -1 (1 - cos)-1. A
source with =
1O thus has an enormous front-to-back ratio, so that an
intrinsically weak source aimed at us may look strong, whereas an
intrinsically strong one aimed away will be weak. When this strong
boosting is combined with an intrinsic luminosity function (many more
weak sources than strong ones), the result is that a flux-limited
sample of beamed sources will consist nearly entirely of objects at
small angles. When this calculation is carried through in detail, it
turns out that the expected distribution of superluminal velocities
has a strong peak near the maximum possible velocity,
vmax = c. Thus
the histogram in Fig. 3 may reflect the
distribution of Lorentz factors, rather than revealing the angular
distribution of superluminal sources.
A more direct way to study these objects is to select a sample on the basis of some ``aspect-independent'' quantity. The superluminal motions will then be oriented at random, and so the measured distribution of velocities should be a direct test of the beaming hypothesis. Several experiments along this line are currently under way. The aspects- independent quantity is taken to be the flux density in the outer lobes; nearly everyone thinks that the outer lobes radiate isotropically. This work is difficult and slow, because the central components are generally weak. The first results from these tests are in crude agreement with the beaming hypothesis: The velocities observed so far are smaller, on average, than those of the strong core-dominated sources.
The superluminal objects include quasars at large redshifts, and they may contain a ``standard velocity,'' that is, the velocity of light. Thus, almost from their discovery, there have been attempts to use them for cosmology. The early work used a ``light echo'' model, but it now is clear that this picture is too simple. It does not easily allow for the observed morphology, especially the asymmetry around the core.
The same objections have been raised against models that use
excitations along magnetic field lines. More recent work has used
models with relativistic beams. If two-jet objects could be found they
should be near the plane of the sky, and then from Eq. (1) v c; that
is, we have recovered the standard velocity. Unfortunately, there are
as yet no reliable two-sided motions. A different method uses the
highest velocities that are measured; these are limited to
vmax
c
and so the top bin in Fig. 3 implies H0
900 km sec-1
Mpc-1. If
there were a reliable physical model from which the Lorentz factor
could be found, then the Hubble constant could be calculated. So far,
though, it has been the other way around; H0 is used
to estimate the
Lorentz factor. Values of found this way generally agree with those
needed to explain the variability and the spectrum.