STARS, CEPHEID VARIABLE
T. Lloyd Evans
Cepheid variable stars are supergiants with luminosities 500-30,000 times greater than that of the Sun, although their surface temperatures are similar to the Sun's temperature. They undergo regular radial pulsations (i.e., the star expands and contracts), with periods mainly in the range 1-50 days, and can be distinguished at great distances. More than 400 Cepheids are known in the Galaxy and about 1000 Cepheids have been found in each of the two nearest galaxies, the Magellanic Clouds, as well as substantial numbers in other nearby galaxies. The close relationship between period and luminosity which was found by Henrietta S. Leavitt in 1912 has given Cepheids a unique role in establishing the distances of the nearer galaxies and hence the distance scale of the universe.
The regularity of the light curve of a Cepheid variable star is matched by that of the radial-velocity curve, which is almost a mirror image of the light curve with minimum radial velocity (i.e., maximum velocity of approach) at light maximum. The light amplitude is typically between 0.5 and 2 magnitudes in visual light and the velocity amplitude usually lies in the range 30-60 km s-1. The first Cepheid velocity curves were measured toward the end of the nineteenth century and were interpreted as the results of orbital motion. It was only after orbits had been computed for a substantial number of Cepheids that it was realized that these orbits were physically implausible.
The pulsation hypothesis gained increasing acceptance after 1910, especially because the surface temperature changes over the cycle. Sir Arthur Eddington's theoretical work from 1917 onwards showed that Cepheids are single stars that undergo radial pulsations because they function as a heat engine. Later work by S.A. Zhevakin, J.P. Cox, Robert F. Christy, and others has provided a deeper understanding of the mechanism. Energy is stored in the form of the second ionization of helium during the compression stage of the cycle and then released as the helium recombines during the expansion stage. The restriction of Cepheid pulsations to stars in a limited temperature range follows from the requirement that the second helium ionization zone lies near the transition from the nearly adiabatic interior, where any driving is almost canceled by an equal amount of damping, to the nonadiabatic exterior where the thin outer layers lack the heat capacity to modulate the outward flow of radiation. The pulsation is a property of the stellar envelope and is independent of the nuclear-energy-generating core.
CLASSICAL AND TYPE II CEPHEIDS
Classical Cepheids are comparatively young stars with masses of several times the solar mass. This follows from their strong concentration toward the plane of the Milky Way and their low space velocities. Their presence in star clusters allows their ages to be estimated as up to about 108 yr. Observations of the Cepheids in the Magellanic Clouds show that the classical Cepheids are confined to a narrow strip in the period-luminosity diagram, whereas the less common Type II Cepheids are fainter than them at a given period. The presence of Type II Cepheids in globular clusters and in the galactic halo population allows their age to be estimated as up to 15 x 109 yr, so that they must be much less massive than the classical Cepheids. The Type II Cepheids can also be distinguished from the classical Cepheids by the shape of the light curves and by spectroscopic peculiarities.
CEPHEID LIGHT CURVES
The light curves of most classical Cepheids are asymmetrical, with a rapid rise to maximum light and a slower fall. The form of the light curve changes with period in a systematic way known as the Hertzsprung progression. A bump appears on the descending branch of the light curve of stars with periods of about a week and is found at earlier phases in stars of successively longer periods so that the bump is near maximum light in stars of 10-day period which may show a double maximum. The bump falls on the rising branch in stars of longer period. Stars of the shortest or longest periods have smooth light curves. The amplitude of the pulsation increases slowly with period up to about 10 days, where there is a drop in amplitude; it then increases more rapidly to longer periods. The bumps may represent an echo of the surface pulsation from the deep interior; an alternative explanation is that they result from a resonance when the second overtone period is about one-half of the fundamental period.
Some Cepheids of short period have nearly sinusoidal light curves with amplitudes of only about 0.5 magnitude. These stars are uncommon in the Galaxy but account for about 10% of the Cepheids known in the Magellanic Clouds. A monumental study by Cecilia Payne-Gaposchkin and Sergei Gaposchkin showed that they are systematically brighter than the period-luminosity relation defined by the stars with asymmetrical light curves. The ratio in periods at a given luminosity is 0.6, which in view of the observational uncertainties is probably identical to the well-defined ratio P1 / P0 = 0.71 found for double-mode Cepheids in the Galaxy. The latter are Cepheids, mostly in the period range P0 = 2.0-4.3 days, whose light curves may be represented as the sum of simultaneous pulsations in the fundamental and first overtone periods of P0 and P1 days, respectively. An analogous situation is found in the RR Lyrae stars in globular clusters.
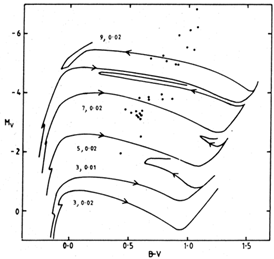
THEORETICAL EVOLUTIONARY TRACKS OF CEPHEIDS
Evolutionary tracks covering the mass range and evolutionary states in
which Cepheids occur have been calculated by Icko Iben, Jr. and
others. The mass range 3-9 M (solar masses) covers all but stars of
very long period. The most important point is that a star may cross
the Cepheid instability strip on the Hertzsprung-Russell (HR) diagram
more than once during its evolution (see
Fig. 1). The star leaves the
main sequence after the exhaustion of H in the core and then expands
to become a red giant while burning H in a shell surrounding the
temporarily inert He core. It crosses the instability strip rapidly on
a Kelvin-Helmholtz or thermal time scale. It climbs the red giant
branch to the red giant tip and after the ignition of He burning in
the core it may make a loop to higher temperature in the HR
diagram. This loop may extend to sufficiently high temperature (or
blue color) to intersect the instability strip, in which case two more
crossings will occur. Core helium burning is a relatively long-lived
evolutionary stage and the star may remain in the instability strip
for much longer, by perhaps a factor of 50, than it did in the first
crossing. The exact location of the blue loops is a function of mass
and of chemical composition, so that above and below the most
favorable mass, the number of Cepheids will decline quickly. The more
massive stars evolve more rapidly in any case, so that the peak
residence time will correspond to a relatively low mass with a decline
in the numbers of longer-period stars which is accentuated by the
relative rarity of massive stars. All the Cepheids at the extremes of
the mass (period) distribution must be on their first crossing of the
instability strip. It has been estimated that they account for about
10% of all Cepheids.
(solar masses) covers all but stars of
very long period. The most important point is that a star may cross
the Cepheid instability strip on the Hertzsprung-Russell (HR) diagram
more than once during its evolution (see
Fig. 1). The star leaves the
main sequence after the exhaustion of H in the core and then expands
to become a red giant while burning H in a shell surrounding the
temporarily inert He core. It crosses the instability strip rapidly on
a Kelvin-Helmholtz or thermal time scale. It climbs the red giant
branch to the red giant tip and after the ignition of He burning in
the core it may make a loop to higher temperature in the HR
diagram. This loop may extend to sufficiently high temperature (or
blue color) to intersect the instability strip, in which case two more
crossings will occur. Core helium burning is a relatively long-lived
evolutionary stage and the star may remain in the instability strip
for much longer, by perhaps a factor of 50, than it did in the first
crossing. The exact location of the blue loops is a function of mass
and of chemical composition, so that above and below the most
favorable mass, the number of Cepheids will decline quickly. The more
massive stars evolve more rapidly in any case, so that the peak
residence time will correspond to a relatively low mass with a decline
in the numbers of longer-period stars which is accentuated by the
relative rarity of massive stars. All the Cepheids at the extremes of
the mass (period) distribution must be on their first crossing of the
instability strip. It has been estimated that they account for about
10% of all Cepheids.
CEPHEID PERIOD DISTRIBUTIONS
The distribution of periods has been found for Cepheids in the Galaxy, the Magellanic Clouds, and several other nearby galaxies. There is inevitably selection in favor of the brighter long-period Cepheids and those of larger amplitude at a given period, but differences between the period distributions in the Galaxy and the two Magellanic Clouds are well established. The distributions in these three systems may be characterized by the shortest periods, the periods that are most common, and the longest periods for fundamental mode pulsators:
| Galaxy | 2.3 days | 5.4 days | 67 days |
| LMC | 1.6 | 3.4 | 135 |
| SMC | 1.1 | 2.9: | 210 |
(The second, third, and fourth columns above list the shortest, maximum frequency peak, and longest periods, respectively.) The maximum frequency peak period in the SMC, about 2.9 days, is uncertain because there is a wide double maximum in the period distribution. There is some doubt as to whether the Cepheid-like stars of the very longest periods are genuine Cepheids or are some other type of variable star. Even so, the overall distributions are very wide and are difficult to account for theoretically unless there is a spread of metal content (abundances of elements heavier than helium) within each galaxy.
The principal difference between the Cepheids in the three galaxies is the successively smaller value of the shortest and maximum frequency peak periods in the order Galaxy-LMC-SMC, which is in order from high to low metal abundance. This is readily explained by the differences in the evolutionary tracks resulting from the differences in composition. The blue loops in the core helium burning stage extend to higher temperature the lower the metal abundance, so that the maximum frequency Cepheids occurs at lower mass and luminosity and shorter period. Stars of lower mass are relatively more numerous, so that a star system of lower metal abundance will contain more Cepheids, other factors being equal. The more metal-deficient Small Magellanic Cloud contains roughly as many Cepheids as the Large Magellanic Cloud whose total mass is four times greater.
CEPHEIDS IN STAR CLUSTERS
The approximately 400 known classical Cepheids in the Galaxy include
only 17 which are well-established members of star clusters and as
these are divided between 14 clusters, there are too few stars in any
one cluster to study the distribution of stars in the
Hertzsprung-Russell diagram. The Magellanic Clouds contain much richer
clusters and NGC 1866 in the Large Magellanic Cloud contains at least
seven Cepheids with periods in the range 2.6-3.5 days. Comparison of
the observed and theoretical HR diagrams leads to an estimated metal
(elements heavier than helium) abundance Z = 0.016, a Cepheid mass of
about 4.9 M , and an age of 86 x 106 yr. There are
still differences in
detail in the numbers and positions, especially of the red giant
stars, between the observed cluster and that which is calculated theoretically.
, and an age of 86 x 106 yr. There are
still differences in
detail in the numbers and positions, especially of the red giant
stars, between the observed cluster and that which is calculated theoretically.
The main value of the Cepheids in the small clusters in the Galaxy is that they may be used to establish the zero point of the period-luminosity relation. The 17 stars noted previously and another 8 of longer period which belong to the loose stellar groups known as associations have been used to establish the zero point to an accuracy of ± 0.1 magnitude, excluding uncertainties in the distance scale for star clusters.
CEPHEIDS IN BINARY SYSTEMS
Our knowledge of the masses of stars is obtained from binary systems.
Spectroscopic orbits need to be obtained for both components of a
binary and the inclination of the orbital plane to the line of sight
must be found or the mass of one component has to be established
independently. The orbital periods of Cepheid binaries are generally
long: The shortest known is the 507-day orbital period of the 9.7-day
variable star S Muscae. This means that the velocity amplitudes are
quite small and that eclipses that would establish the orbital
inclination are unlikely to occur. The mass of the companion must be
deduced from its spectrum. The light of the Cepheid is always dominant
at visible wavelengths so the spectrum of the companion, which is
usually a much hotter B star, is only readily distinguishable in the
far ultraviolet. This means that observations must be made from a
satellite. A few estimates of around 5-6 M for Cepheids of periods of
4-10 days are available so far, in broad agreement with the mass
estimates from evolutionary tracks. The latter have generally been
found to give larger masses than methods based on the pulsation
properties of the stars and more precise dynamical mass estimates are
needed to clarify the situation.
for Cepheids of periods of
4-10 days are available so far, in broad agreement with the mass
estimates from evolutionary tracks. The latter have generally been
found to give larger masses than methods based on the pulsation
properties of the stars and more precise dynamical mass estimates are
needed to clarify the situation.
The limiting orbital period below which a Cepheid on its first crossing of the instability strip would suffer disturbance to its evolution is about 20 days but a Cepheid crossing the instability strip for the second time on a blue loop has previously expanded to a much larger radius at the red giant tip. The minimum period to avoid overflowing the Roche lobe with consequent severe mass loss is several hundred days in this case. The longer periods of all the Cepheid binaries studied to date are in accordance with the theoretical estimate that most are on their second or a subsequent crossing of the instability strip.
-
Christy, R.F. (1966). Pulsation theory. Ann. Rev. Astron.
Ap. 4 353.
Cox, A.N. (1980). The masses of Cepheids. Ann. Rev. Astron.
Ap. 18 15.
Cox, J.P. (1980). Theory of Stellar Pulsation. Princeton University
Press, Princeton.
Fernie, J.D,. (1990). The structure of the Cepheid instability strip.
Astrophys. J. 354 295.
Payne-Gaposchkin, C. and Gaposchkin, S. (1966). Relation of light
curve to period for stars in the Small Magellanic Cloud. Vistas in
Astronomy 8 191.
Pel, J.W. (1985). Fundamental parameters of Cepheids. In
Cepheids: Theory and Observations, B.F. Madore, ed.
Cambridge University Press, Cambridge, p. 1.
Zhevakin, S.A. (1963). Physical basis of the pulsation theory of
variable stars. Ann. Rev. Astron. Ap. 1 367.
See also Star Clusters, Globular, Variable Start; Stars, BL
Herculis, W W Virginis, and RV Tauri Types; Stars, Cepheid Variable,
Dwarf; Stars, Cepheid Variable, Period-Luminosity Relation and Distance
Scale; Stars, Pulsating, Overview; Stars, Pulsating, Theory.