3. DISTRIBUTION OF GALAXIES AND CLUSTERS

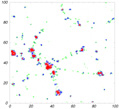
In Figure 1 I show the distribution of galaxies of various luminosity in a volume-limited sample through the Virgo, Coma and Hercules superclusters. We use supergalactic coordinates Y and Z in km/s, respectively, in a sheet 0 X < 10 h^-1 Mpc. Bright galaxies (M_B - 20.3) are plotted as red dots, galaxies -20.3 < M_B - 19.7 as black dots, galaxies -19.7 < M_B - 18.8 as open blue circles, galaxies -18.8 < M_B - 18.0 as green circles (absolute magnitudes correspond to Hubble parameter h = 1). High-density regions are the Local, the Coma and the Hercules superclusters in the lower left, lower right and upper right corners, respectively. The long chain of galaxies between Coma and Hercules superclusters is called the Great Wall. Actually it is a filament. For comparison, the distribution of particles in a 2-dimensional simulation is also plotted in a box of side-length 100 h^-1 Mpc. Different colors indicate the density value of the particle environment. Particles in voids (density < 1) are shown as black dots; particles in the density interval 1 < 5 form filaments of galaxies (orange dots); particles with densities 5 < 10 (green dots) form groups of galaxies; particles with 10 < 20 (blue dots) form clusters; and particles with 20 (red dots) are in very rich clusters. Densities are expressed in units of the mean density in the simulation; they are calculated using a smoothing length of 1 h^-1 Mpc. Three-dimensional simulations have similar behaviour. This Figure emphasizes that particles in high-density regions simulate matter associated with galaxies, and that the density of the particle environment defines the type of the structure. In both Figures we see the concentration of galaxies or particles to clusters and filaments, and the presence of large under-dense regions. There exists, however, one striking difference between the distribution of galaxies and simulated particles - there is a population of smoothly distributed particles in low-density regions in simulations, whereas in the real Universe voids are completely empty of any visible matter. This difference is due to differences of the evolution of matter in under- and over-dense regions.

Figure 1. The distribution of galaxies (upper panel), and particles in a 2-D simulation (lower panel). For explanations see text

Zeldovich [60] and Einasto, Jõeveer & Saar [24] have shown that the density evolution of matter due to gravitational instability is different in over- and under-dense regions. The evolution follows approximately the law

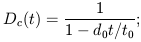
(1)

where d₀ is a parameter depending on the amplitude of the density fluctuations. In over-dense regions d₀ > 0, and the density increases until the matter collapses and forms pancake or filamentary systems [6] at a time t₀; thus the formula can be applied only for t t₀. In under-dense regions we have d₀ < 0 and the density decreases, but never reaches zero (see Figure 2). In other words, there is always some dark matter in under-dense regions. At the time when over-dense regions collapse the density in under-dense regions is half of the original (mean) density. In order to form a galaxy the density of matter in a given region must exceed a certain critical value [44], thus galaxies cannot form in under-dense regions. They form only after the matter has flown to over-dense regions: filaments, sheets, or clusters; here the formation occurs in situ.

Figure 2. Left: Density evolution in over- and under-dense regions (solid and dashed lines, respectively) for two epochs of caustics formation. Right: Density perturbations of various wavelengths. Under-dense regions (D < 1) become voids; strongly over-dense regions (D > 1.3) - superclusters (cluster chains); moderately over-dense regions (1 < D < 1.3) - filaments of groups and galaxies.

Consider the distribution of matter as a superposition of several sinusoidal waves of amplitude a_i and period p_i around the mean density D_m

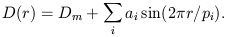
(2)

Gravitational instability determines the evolution of these density perturbations: large high over-dense regions become superclusters; weakly over-dense regions become small filaments of galaxies and groups; under-dense regions become voids, see Figure 2. The fine structure of superclusters is defined by perturbations of medium wavelength, the structure of clusters by small-scale perturbations.