6. COSMOLOGICAL MODELS

The power spectra of matter and the angular spectra of CMB can be calculated for a set of cosmological parameters using the CMBFAST algorithm [50]; spectra are COBE normalized. The cluster abundance and mass distribution functions can be calculated by the Press-Schechter [44] algorithm. We have used these algorithms to test how well cosmological parameters are in agreement with these descriptive functions.

One problem in comparing cosmological models with observations is related to the fact that from observations we can determine the power spectra and correlation functions of galaxies and clusters of galaxies, but using models we can do that for the whole matter. Power spectra of galaxies and matter are related through the bias parameter. There exist various methods to estimate the bias parameter, using velocity data. Here we use another method which is based on the numerical simulation of the evolution of the Universe. During dynamical evolution matter flows away from low-density regions and forms filaments and clusters of galaxies. This flow depends slightly on the density parameter of the model. The fraction of matter in the clustered population can be found by counting particles with local density values exceeding a certain threshold. To separate void particles from clustered particles we have used the mean density, since this density value divides regions of different cosmological evolution, see eq. (1). Hydrodynamical simulations by Cen & Ostriker [12] confirmed that galaxy formation occurs only in over-dense regions.

We express the epoch of simulations through the ₈ parameter, which was calculated by integrating the power spectrum of matter. It is related to the observed value of (₈)_gal by the equation (compare with eq. (5, 6))

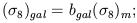
(11)

here we assume that b_gal = b_c. This equation, and the observed value of (₈)_gal, yields one equation between (₈)_m and b_c (or F_gal); it is shown in the upper left panel of Figure 6 by a bold line with error corridor. The other equation is given by the growth of F_gal with epoch. For two LCDM models with density parameter _m 0.4 the growth of F_gal is shown by dashed curves in the upper left panel of Figure 6 [23]. By simultaneous solution of both equations we found all three quantities of interest for the present epoch: rms density fluctuations of matter (₈)_m = 0.64 ± 0.06, the fraction of matter in the clustered population, F_gal = 0.70 ± 0.09, and the biasing parameter b_gal = 1.4 ± 0.1.

Figure 6. Upper left: the fraction of matter in the clustered population associated with galaxies as a function of 8 for 2 LCDM models (dashed curves); and the relation between Fgal and (8)m (bold solid line). Upper right: the biasing parameter needed to bring the amplitude 8 of the model into agreement with the observed 8 for galaxies and for LCDM and MDM models with various matter density m and HDM density, n. The dashed box shows the range of the bias parameter allowed by numerical simulations of the evacuation of voids. Lower left: power spectra of LCDM models with various m. Lower right: angular spectra of CMB for LCDM and MDM models for various m.

The CMBFAST algorithm yields for every set of cosmological parameters the ₈ value for matter. It is calculated using the linear growth model of density perturbations. From observations we know this parameter for galaxies, (₈)_gal. Using eq. (11) we can calculate the biasing parameter b_gal, needed to bring the theoretical power spectrum of matter into agreement with the observed power spectrum of galaxies. This parameter must lie in the range allowed by numerical simulations of the evolution of structure. Results of calculations for a range of _m are shown in the upper right panel of Figure 6, using the Hubble constant h = 0.65, baryon density _b = 0.05, and HDM densities _n = 0.00, 0.05, 0.10. The biasing parameter range shown in the Figure is larger than expected from calculations described above; this range corresponds to the maximum allowed range of the fraction of matter in the clustered population expected from analytic estimates of the speed of void evacuation.

Power spectra for LCDM models (_n = 0; 0.2 _m 0.5) are shown in the lower left panel of Figure 6. We see that with increasing _m the amplitude of the power spectrum on small scales (and respective ₈ values) increases, so that for high _m the amplitude of the matter power spectrum exceeds the amplitude of the galaxy power spectrum. This leads to bias parameter values b 1. Such values are unlikely since the presence of matter in voids always increases the amplitude of the galaxy power spectrum relative to the matter spectrum. If other constraints demand a higher matter density value, then the amplitude of the matter power spectrum can be lowered by adding some amount of HDM. However, supernova and cluster X-ray data exclude density values higher than _m 0.4; thus the possible amount of HDM is limited. The lower right panel of the Figure 6 shows the angular spectrum of temperature anisotropies of CMB for different values of the density parameter _m. We see that a low amplitude of the first Doppler peak of the CMB spectrum prefers a higher _m value: for small density values the amplitude is too high. So a certain compromise is needed to satisfy all data.

The cluster mass distribution for LCDM models 0.2 _m 0.3 is shown in the left panel of Figure 7. We see that low-density models have a too low abundance of clusters over the whole range of cluster masses. The best agreement with the observed cluster abundance is obtained for a LCDM model with _m = 0.3, in good agreement with direct data on matter density. In this Figure we show also the effect of a bump in the power spectrum, which is seen in the observed power spectrum of galaxies and clusters [22]. Several modifications of the inflation scenario predict the formation of a break or bump in the power spectrum. The influence of the break suggested by Lesgourgues, Polarski and Starobinsky [32] was studied by Gramann and Hütsi [28]. Another mechanism was suggested by Chung [13]. To investigate the latter case we have used a value of k₀ = 0.04 h Mpc^-1 for the long wavenumber end of the bump, and a = 0.3 - 0.8 for the amplitude parameter. Our results show that such a bump only increases the abundance of very massive clusters. In the right panel of Figure 7 we show the cluster abundance constraint for clusters of masses exceeding 10¹⁴ solar masses; the curves are calculated for LCDM and MDM models with _n = 0.00, 0.05, 0.10. We see that the cluster abundance criterion constrains the matter and HDM densities in a rather narrow range.

Figure 7. Left: cluster mass distribution for LCDM models of various density m, with and without a Chung bump of amplitude a = 0.5. Right: cluster abundance of LCDM and MDM models of various density of matter m and hot dark matter n

The power spectra of LCDM models with and without the Starobinsky break are shown in the upper left panel of Figure 8; these models were calculated for the parameter = _mh = 0.20. In the case of the spectrum with a bump we have used MDM models as a reference due to the need to decrease the amplitude of the spectrum on small scales; these spectra are shown in the upper right panel of Figure 8. Power spectra are compared with the observed galaxy power spectrum [22] and with the new cluster power spectrum [38], reduced to the amplitude of the galaxy power spectrum. Also the matter power spectrum is shown, for which we have used a biasing factor b_c = 1.3 [23]. We see that the Starobinsky model reproduces well the matter power spectrum on small and intermediate scales, but not the new data by Miller & Batuski. The modification by Chung [13] with amplitude parameter a = 0.3 fits well all observational data. The cluster mass distribution for the Chung model is shown in the lower left panel of Figure 8, and the angular spectrum of CMB temperature fluctuations in the lower right panel of Figure 8. In order to fit simultaneously the galaxy power spectrum and the CMB angular spectrum we have used a tilted MDM model with parameters n = 0.90, _b = 0.06, _n = 0.05, and _m = 0.4.

Figure 8. Upper left: power spectra of a LCDM model with and without Starobinsky modification. Upper right: power spectra of MDM models with and without Chung modification. Lower left: cluster mass distributions for MDM models with and without Chung modification. Lower right: angular power spectra of tilted MDM models with and without Chung modification (amplitude parameter a = 0.3).

BOOMERANG and MAXIMA I data have been used in a number of studies to determine cosmological parameters [7, 17, 30, 56, 59]. In general, the agreement between various determinations is good; however, some parameters differ. There is a general trend to interpret new CMB data in terms of a baryon fraction higher than expected from the nucleosynthesis constrain; h²_b = 0.03. Tegmark & Zaldarriaga [56] suggested a relatively high matter density, h²_m = 0.33. On the other hand, velocity data suggest a relatively high amplitude of the power spectrum, _8m^0.6 = 0.54, which in combination with distant supernova data yields _m = 0.28 ± 0.10, and ₈ = 1.17 ± 0.2 [7].

Our analysis has shown that a high value of the density of matter, _m > 0.4, is difficult to reconcile with current data on supernova and cluster abundances. Similarly, a high amplitude of the matter power spectrum, ₈ > 1, seems fairly incompatible with the observed amplitude of the galaxy power spectrum and reasonable bias limits. This conflict can be avoided using a tilted initial power spectrum, and a MDM model with a moderate fraction of HDM, as discussed above. The best models suggested so far have 0.3 _m 0.4, 0.90 n 0.95, 0.60 h 0.70, _n 0.05. Matter density values lower than 0.3 are strongly disfavoured by the cluster abundance constraint, and values higher than 0.4 by all existing matter density estimates. This upper limit of the matter density, in combination with the cluster abundance and the amplitude of the power spectrum, yields an upper limit to the density of hot dark matter. We can consider this range of cosmological parameters as a set which fits well all constraints. This set of cosmological parameters is surprisingly close to the set suggested by Ostriker & Steinhardt [40]. Now it is supported by much more accurate observational data.

Acknowledgements

I thank M. Einasto, M. Gramann, V. Müller, A. Starobinsky, E. Saar and E. Tago for fruitful collaboration and permission to use our joint results in this review, and H. Andernach for suggestions to improve the text. This study was supported by the Estonian Science Foundation grant 2625.