3. STAR FORMATION HISTORIES

One of the most active areas of relevance to understanding the rate at which galaxies assemble is concerned with determining the cosmic star formation history. The idea is simple enough. A systematic survey is conducted according to some property that is sensitive to the on-going rate of star formation. The volume-average luminosity density is converted into its equivalent star formation rate averaged per unit co-moving volume and the procedure repeated as a function of redshift to give the cosmic star formation history _*(z). In this section we will explore the uncertainties and also the significance of this considerable area of current activity in terms of the constraints they provide on theories of galaxy formation.

The joint distribution of luminosity L and redshift z, N(L, z), for a flux-limited sample permits the construction of the luminosity function (L) according to procedures which are reviewed by Efstathiou, Ellis & Peterson (1988) and compared by Ellis (1997). The luminosity function is often characterised according to the form defined by Schechter (1976), viz:

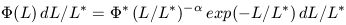
(3.3)

in which case the integrated number of galaxies per unit volume N and the luminosity density _L then becomes:

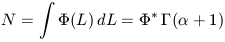
(3.4)

and

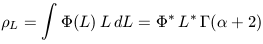
(3.5)

and the source counts in the non-relativistic case, applicable to local catalogs, is:

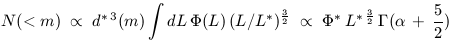
(3.6)

Frequently-used measures of star formation in galaxies over a range of redshift include rest-frame ultraviolet and blue broad-band luminosities ([Lilly et al 1995, Steidel et al 1996, Sullivan et al 2000]), nebular emission lines such as H (Gallego et al 1995, Tresse & Maddox 1998, Glazebrook et al 1999), thermal far-infrared emission from dust clouds ([Rowan-Robinson et al 1997, Blain et al 1999]) and, most recently, radio continuum emission ([Mobasher et al 1999]).

Since only a limited range of the luminosity function centered on L* is reliably probed in flux-limited samples, a key issue is how well the integrated luminosity density can be determined from such surveys. In the Schechter formalism, equations [3.4] and [3.5] show that whilst N would diverge for < -1, the luminosity density is convergent unless < -2.

Figure 4 shows the local rest-frame ultraviolet (2000 Å) luminosity function from Sullivan et al (2000) whose faint end slope = -1.6 is markedly steeper than that found for samples selected in the near-infrared ([Mobasher et al 1993, Gardner et al 1997, Cole et al 2000b]) (where -1). This contrast in the luminosity distribution of young and old stellar populations is an important result which emphasizes the relatively weak connection between stellar mass and light and implies there may be significant uncertainties in the estimation of integrated luminosity densities for star-forming populations.

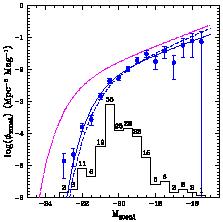
Figure 4. The luminosity function for galaxies selected at 2000 Å from the recent survey of Sullivan et al (2000). The histogram and associated numbers indicate the absolute magnitude distribution observed which is corrected by volume and k-correction effects to give the data points. The dotted curve illustrates the considerable effect of extinction as gauged by Balmer decrements determined individually for those galaxies with emission lines. Such uncertainties translate in factors of two uncertainty in the local UV luminosity density.

Kennicutt (1998) carefully reviewed the relationships between the various observational diagnostics listed above and the star formation rate. Clearly a major uncertainty in any transformation based on the ultraviolet/optical continuum or nebular emission line measures is the likely presence of absorbing dust (Figure 4). Other uncertainties include the form of the initial stellar mass function and the nature of the star formation history itself.

Some of these uncertainties are quite imponderable and the only way to estimate their effect in typical populations is to undertake a comparison of the various diagnostics for the same sample. Sullivan et al (2000) compared UV and H-based estimators for their local balloon-based UV-selected sample and Glazebrook et al (1999) undertook a similar comparison for a restricted incomplete sample of high redshift galaxies (drawn from a I-selected sample). Bell & Kennicutt (2000) independently examined some of Sullivan et al's conclusions based on a smaller local sample with satellite UV fluxes. The comparison analysed by Sullivan et al is shown in Figure 5. Although an overall linear relation is observed the scatter is quite considerable, greater than accountable from observational errors. The uncertainties would appear to be alarming in view of the fairly modest trends claimed in _SFR(z) (see below).

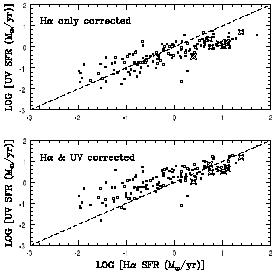
Figure 5. Star formation rates derived from UV (2000 Å) continua versus those derived from H fluxes from the local survey of Sullivan et al (2000, open squares) and the z samples of Glazebrook et al (1999, large stars). For the Sullivan et al sample, extinction corrections were derived from individual Balmer decrements assuming Case B recombination and applied to the H fluxes in the upper panel and both estimates in the lower panel.

Figure 6 shows a recent estimate of the cosmic star formation history drawn from various surveys ([Blain 2000]). There appears to be a marked increase in activity over 0 < z < 1 with a possible decline beyond z >2. Although, inevitably perhaps, attention has focused on the case for the high redshift decline, even the strong rise to z 1 remains controversial. Originally proposed independently by Lilly et al (1995) and Fall et al (1996), revised estimates for the local luminosity density ([Sullivan et al 2000]) and independent surveys ([Cowie et al 1999]) have challenged the rapidity of this rise. Part of the problem is that no single survey permits a self-consistent measurement of _SFR over more than a very limited range in z. Most likely, therefore, much of the scatter in Figure 6 is simply a manefestation of the kinds of uncertainties discussed above in the context of Sullivan et al's survey.

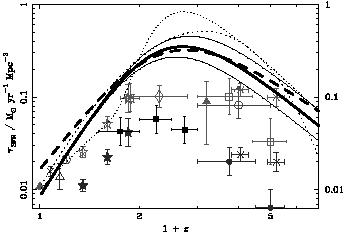
Figure 6. The history of recent star formation from the recent compilation of Blain (2000). Data points are taken from a variety of sources referenced in that article. Thick solid and dashed lines represent trends expected from simple luminosity evolution and hierarchical models, respectively. It is clear there is considerable observational scatter at all redshifts, not just beyond z 1 as often assumed.

Beyond z 2, the available star formation rates have been derived almost exclusively from UV continua in Lyman break galaxies selected by their `dropout' signatures in various photometric bands ([Madau et al 1996, Steidel et al 1996, Steidel et al 1999]) and from currently scant datasets of sub-mm sources interpreted assuming thermal emission from dust heated by young stars ([Blain et al 1999, Barger et al 1999b]). There has been much discussion on the possible disparity between the estimates derived from these two diagnostics (which other lecturers will address). Two points can be made: firstly, the measured UV luminosity densities will clearly underestimate the true values given likely extinctions. Secondly, the sample of sub-mm sources with reliable redshifts remains quite inadequate for luminosity density estimates in the sense described above. Most of the constraints arise from modelling their likely properties in a manner consistent with their source counts and the integrated far-infrared background.

Have we become over-obsessed with determining the cosmic star formation history? Observers are eager to place their survey points alongside others on the overall curve and different groups defend their methods against those whose data points disagree. We should consider carefully what role this cosmic star formation history plays in understanding how galaxies form?

Clearly, the prime conclusion we can draw from Figure 6 is that the stars which make the galaxies we see today formed continuously over a very wide redshift range. This may seem such an obvious deduction that it hardly merits stating but it is important to stress the absence of any obvious detectable `epoch of star formation' as was once imagined ([Eggen, Lynden-Bell & Sandage 1962, Frenk et al 1988]). Hierarchical modelers were quick to point out (e.g. [Baugh et al 1998]) that they predicted extended star formation histories as early as 1990 ([White & Frenk 1991]). It is certainly true that a continuous assembly of galaxies is a major feature of these models and thus one supported by the data.

However, what about the quantitative form of Figure 6 which remains so difficult to pin down: does the shape of the curve really matter? Firstly, we should recognise that the luminosity density integrates over much detailed astrophysics that may be important. A particular _SFR at a given redshift could be consistent either with a population of established massive sources undergoing modest continous star formation or a steep luminosity function where most of the activity is in newly-formed dwarf galaxies. In terms of structure formation theories, these are very different physical situations yet that distinction is lost in Figure 6.

Secondly, theoretically, the cosmic star formation history is not particularly closely related to how galaxies assemble. It is more sensitive to the rate at which gas cools into the assembling dark matter halos, a process of considerable interest but which involves a myriad of uncertain astrophysical processes (Figure 7) which are fairly detached from the underlying physical basis of say the hierarchical picture. In support of this, we should note that Baugh et al (1999) were able, within the same -dominated CDM model, to `refine' their earlier prediction to match new high redshift datapoints revealing a much less marked decline beyond z 2.

Figure 7. An illustration of the complex physical processes governing the star formation rate of a young galaxy (courtesy of Carlos Frenk). Star formation is governed by the rate at which baryonic gas cools and falls into dark matter halos and this is inhibited by heating, e.g. from supernovae. The precise form of the cosmic star formation history gives us more insight into the interplay between these processes, integrated over all star-forming galaxies, than in distinguishing between various forms of structure formation (e.g. hierarchical vs. monolithic).