Copyright © 1979 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 1979. 17:
135-87 Copyright © 1979 by Annual Reviews. All rights reserved |
Three basic methods can be used to determine the mass and mass-to-light ratio of a spheroidal stellar system. The first of these utilizes the global virial theorem, extensively discussed by Poveda (1958):
where I is the moment of inertia, T the kinetic energy,
and
where the potential energy
M, R are the total mass and radius, M (r) is the mass
contained within
a sphere of radius r, and <V2> is the
mass-weighted average of the
square of the space velocities of the stars relative to the center of
mass of the galaxy.
Equations (3) and (4) involve theoretical parameters which are far
removed from observed quantities. <V2> for example is usually
estimated from the observed line-of-sight velocity dispersion (
The virial theorem thus leads to uncertain results basically because
it treats the whole galaxy, including the poorly understood outer
regions. To circumvent this difficulty, King
(King & Minkowski
1972
and in preparation) has devised a second method to determine M / L; this
method is based on stellar hydrodynamical equations applied to the
core only. The observational data required include the central surface
brightness, core radius (the point where surface brightness drops to 1/2
of central value), and core line-of-sight velocity dispersion. From
these one determines the core density and core mass-to-light ratio.
Total mass is not derived. The method assumes only that the nuclear
velocity distribution is Gaussian and isotropic with constant
King's formula contains an explicit correction for rotational motion
based on the observed ellipticity. However, several studies (e.g.
Bertola & Capaccioli
1975,
Illingworth 1977,
C. Peterson 1978)
have shown that even flattened ellipticals rotate very slowly and are
almost completely pressure supported; rotational corrections should
therefore be small.
Binney (1976) and
Miller (1978)
have presented
alternative models for elliptical galaxies having anisotropic velocity
dispersions. These models imply a correction to our assumption of an
isotropic velocity distribution in the core, but the effect should
again be small.
The last method for determining M / L in E and S0 galaxies is the most
straightforward: find a test particle in circular motion about the
spheroidal component. This approach is applicable to the stellar disks
of S0 galaxies and to gas in orbit about an elliptical [NGC 4278 is
apparently such a galaxy
(Knapp et al. 1978)].
For S0 disks
seen directly edge on, the observed rotational velocity must be
increased by 30-40% to correct for stars at large spatial radii
projected along the line-of-sight
(Bertola &
Cappaccioli 1977,
1978).
Burbidge & Burbidge
(1975)
summarized the results on M / LB in
early-type galaxies through 1969. Their mean value was 19.7, for a
variety of objects and techniques.
King & Minkowski
(1972)
reported values of 7-20 for luminous elliptical galaxies based on King's method
applied to the cores and utilizing Minkowski's velocity dispersions.
Since this early work, the trend in M / LB has been
generally downward
owing to two factors: remeasurements of velocity dispersions
significantly smaller than earlier values, and the general adoption of
core analyses in place of the global virial theorem. It is not easy,
however, to summarize these recent results because there is still
significant disagreement between various groups as to the correct
measurement of
If these systematic differences in
Determinations of velocity dispersions for normal elliptical
galaxies have revealed two possible regularities. Both FJ and
Sargent et al. (1977)
found that
Using a method rather different from those above,
Ford et al. (1977)
have estimated the mass of M32 from motions of planetary nebulae far
from the nucleus. Their result is 4.3 x 108 M
The nucleus of M87 differs significantly from other ellipticals in
having a bright central luminosity spike and a rapid decline in
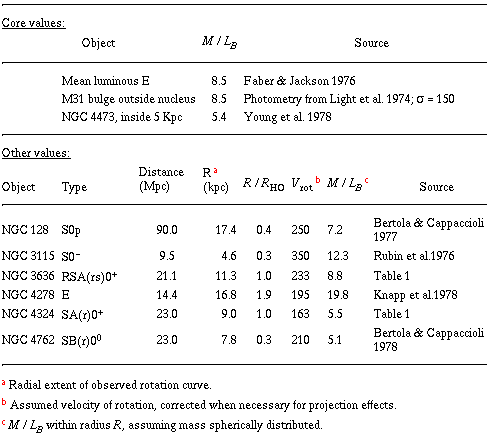
Recent results for M / LB among early-type galaxies
(corrected to the M / L system of the preceding section) appear
in Table 3. The first
group contains objects for which nuclear values of M /
LB have been
measured using King's method or a related treatment. The mean value
obtained by Faber and Jackson is 8.5 for 10 galaxies, while the value
of 8.5 for the inner bulge of M31 is new in this review. The second
group consists of galaxies for which the circular rotation of test
particles can be measured. The mass and M / LB within
radius R have been
computed assuming a spherically symmetric mass distribution as in the
preceding section.
Taken at face value, these data suggest that there is no gross
increase in M / LB from the core to the Holmberg
radius. This conclusion
is supported by the tendency of velocity dispersions to decrease away
from the nucleus in M32
(Ford et al. 1977), NGC 3379 and NGC 4472
(FJ), and NGC 4486
(Sargent et al. 1978),
leading to constant M / L in
the inner regions. On the other hand,
In summary, rotation curve data indicate that M / LB
within the
Holmberg radius is approximately 10 for S0's. This number is entered
in Table 2. No comparable estimate
for E's can be given at this time
owing to inadequate data on the velocity dispersions away from the nuclei.
Of great importance is the question whether a strong increase in M / L
occurs beyond the Holmberg radius, as seems to be the case with
spirals. The evidence on this point is fragmentary but highly
suggestive of dark envelopes around early-type galaxies as well.
NGC 4278 is the only galaxy in Table 1
for which rotation measurements
extend beyond RHO, and its M / LB
seems significantly higher than the others.
Faber et al. (1977)
found no decrease in the velocity
dispersion in the halo of cD galaxy Abell 401 at a radius of 44 kpc,
but the accuracy of the measurement was not high.
Dressler & Rose (1979)
have detected an actual increase in
All these data point strongly to the existence of dark matter around
at least some elliptical galaxies. With the recent increased
availability of efficient two-dimensional detectors for spectroscopy,
additional information on the dynamics of the outer regions of
elliptical galaxies should soon be forthcoming. Ultimately, radial
velocities of globular clusters will be used to probe the structure of
spheroidal systems at very large radii, but these observations seem to
lie just beyond the capabilities of present equipment.
the
gravitational potential energy
(Limber 1959).
For a galaxy in
equilibrium, the left-hand side vanishes. Let us assume further that the
galaxy is spherical and nonrotating and that the kinetic energy of each
star per unit mass is independent of mass. Then
is
given by
) in
the nucleus by assuming that 2 is constant throughout the galaxy, an
assumption usually not supported by any observational data. The
estimate of the total potential energy is likewise subject to great
uncertainty. It is generally assumed that the light distribution is an
adequate tracer of the mass and that the luminosity profiles of most
ellipticals are similar and are adequately described by empirical
expressions, such as the R1/4 law of
de Vaucouleurs (1948)
(see also
Young 1976).
The integral in (4) is then = -0.33 G M2 Re, where
Re is
the isophotal radius containing half the light (and mass). This
approach assumes that the outer structure of the galaxy obeys de
Vaucouleur's law. In fact, there seem to be significant departures
from de Vaucouleur's law in the outer profiles of elliptical galaxies
which correlate with environment
(Kormendy 1977b,
Strom & Strom 1978).
Furthermore, the total light in the envelopes of some cD
ellipticals shows no sign of converging to a finite value
(Oemler 1976,
Carter 1977),
making the determination of Re operationally
impossible. Finally, if ellipticals contain appreciable amounts of
dark material which is more extended than the luminous material,
Re as
determined for the stars alone may have no connection with the true
mass distribution of the galaxy.
over
the core region, in agreement with the properties of model star
clusters whose cores closely resemble the nuclear regions of
elliptical galaxies
(King 1966).
Young et
al. (1978) and
Sargent et al. (1978)
have developed a similar formalism which is applicable to
regions outside the core.
. The two largest
sets of data available are those of
Faber & Jackson
(1976) (FJ) and
Sargent, Young and coworkers (SY)
(Sargent et al. 1977,
1978,
Young et al. 1978).
Although it seemed
initially that the values of FJ exceeded those of SY by 28%, new
measurements (S. Faber, unpublished,
Schechter & Gunn 1979)
now make
it seem likely that the two systems agree within 10%. In comparison to
these results, however, the measurements of
Williams (1977), Morton
and co-workers
(Morton & Chevalier
1972,
1973,
Morton et al. 1977),
and
de Vaucouleurs (1974)
average about 35% smaller. This comparison is quite uncertain, however,
because the number of objects in common is in all cases very small.
are taken into account, one
finds that the agreement between investigators is good, with M /
LB typically 5-10.
Sargent et al. (1977)
found substantially higher M / LB
for elliptical galaxies but did so by applying the virial theorem to
the entire galaxy assuming constant . Since was
available only for
the core, we believe that an analysis based only on the measured core
quantities is preferable.
increased with total galaxy luminosity
approximately as LB1/4. For a sample of
ellipticals with core radii and
central surface brightness determined by I.R. King (unpublished), FJ
derived power-law correlations between luminosity, core radius, and
central surface brightness (see also
Kormendy 1977b).
Using these
correlations plus the L1/4 law for velocity
dispersions, FJ found that
M / LB increased with luminosity as
L1/2.
Schechter & Gunn
(1979) found
no such correlation, based on a published subset of King's data
(King 1978).
However, the published data were not corrected for seeing
effects, unlike the unpublished list used by FJ. This difference
apparently accounts for the discrepancy.
, from which M /
LB = 1.8.
This result would seem to be consistent with the possibility noted
above that M / LB is smaller in less luminous ellipticals.
just outside the spike
(Young et al. 1978,
Sargent et al. 1978).
A mass
with very high M / L, perhaps even a black hole, apparently exists in
the middle of the core. Since very few elliptical galaxies have been
studied with such high spatial resolution, it is not known whether
such cases are common.
does not decline with radius
in NGC 4473
(Young et al. 1978).
Schechter and Gunn
find that is
basically constant in 12 more ellipticals, but their measurements
extend to only a few core radii.
out to 100 kpc in the
halo of the cD galaxy Abell 2029 with much better data, implying a
strong increase in the local mass-to-light ratio. Finally, we mention
the novel mass determination of M87 based on the assumption that the
X-ray emission centered on M87 is due to thermal bremsstrahlung from
isothermal gas in hydrostatic equilibrium within the potential well of
the galaxy
(Bahcall & Sarazin 1977,
Mathews 1978).
Mathews finds in this case that the total mass of M87 exceeds 1013
M and the total
M / LB is several hundred.