3.3. Local dE's and dark matter

Much of the recent upsurge in dE-related research is due to the problem of dark matter (hereafter DM). With decreasing luminosity, galaxies appear to become increasingly dominated by DM (e.g., Kormendy 1988). The dE (``dwarf spheroidal'') companions of our Galaxy, which include the intrinsically faintest galaxies known, have thus become prime targets for the study of DM. The first indication of DM in the local dwarfs is due to Aaronson (1983). His bold announcement of an unusually high velocity dispersion in Draco (based on only three stars) has essentially stood the test of time. In the following we give a brief account of the present status of the search for DM in the local dE's, drawing on the excellent reviews of Mateo (1994), Pryor (1994), and Gerhard (1994) delivered at the recent ESO/OHP workshop on ``Dwarf Galaxies'' (but see also Pryor 1992, and Mateo et al. 1993).

The observational task is formidable: one has to measure precise radial velocities (with errors smaller than 10 km s^-1) for as many as possible, apparently faint (V > 17.5) and weak-lined (low-metallicity) stars. Nevertheless, measurements have now been made for all but one (Leo I) of the eight dE companions of the Galaxy, with varying quantity (number of stars) and quality of data. With the exception of the best-studied Fornax system (Paltoglou and Freeman 1987), the only kinematic datum available is the central , which is typically 10 km s^-1. There is little room left for doubts about the reality of the stellar movements. The only severe problem is contamination with binary stars, which can in principle be solved by finding the binaries through repeat measurements. Multi-epoch observations for some of the dwarfs suggest a binary frequency for giant stars of 10 - 15%, which has little (though not negligible) effect on (Mateo 1994).

Under the most simple assumptions that (1) mass follows light, and (2) the velocity distribution is isotropic, the calculation of a central mass density, ₀, and a mass-to-light ratio, M / L, is straightforward by ``King's method'' (King and Minkowski 1972), also called ``core-fitting'' (Richostone and Tremaine 1986). Present typical uncertainties in the photometric parameters (µ₀ and r_c) and distances of the dwarfs, in addition to a 20% uncertainty in , introduce errors of up to 50% in ₀ and M / L. The derived ₀ values are generally in the range 0.1-1 M pc^-3, while M / L ranges from 5 (Fornax) to > 100 for Draco and Ursa Minor. As M / L 2 for globular clusters, the presence of large amounts of dark matter is clearly indicated. There is a strong correlation betwen M / L and total luminosity, as shown in Fig. 5 (left panel): the less luminous a dwarf the higher its M / L. This is the above-mentioned fundamental-plane relation for dwarf ellipticals, M / L L^-0.4. Interestingly, the total masses of the dwarfs derived under these simplified assumptions is always a few times 10⁷ M, which Mateo et al. (1993) suggest is a minimal mass for dark halos. From the start (Aaronson 1983; Lin and Faber 1983), the dark halos of the dwarfs were used to put constraints on the neutrino mass, and essentially to exclude neutrinos as DM constituents (Gerhard and Spergel 1992a).

However, there is no reason (beyond simplicity) to assume that mass follows light in the dwarfs; spiral galaxies clearly suggest that the dark halos are much more extended than the visible parts. Second, the lack of rotation (see above) manifestly shows that the assumption of velocity isotropy cannot be correct. Are there any constraints on the potential and distribution function of the dwarfs? It has been shown that not even perfect knowledge of the surface brightness and velocity dispersion profiles of a stellar system can uniquely determine its potential (Binney and Mamon 1982; Merritt 1987; Dejonghe and Merritt 1992). Only the most sophisticated use of the entire information contained in the positions and velocities of 1000 stars per galaxy might remove that indeterminacy in the future (Pryor 1994). At present lower limits on ₀ and M / L can be obtained by exploring the allowed parameter space with 2-component models (Pryor and Kormendy 1990; Lake 1990), and by applying the virial theorem (Merritt 1987). The minimal ₀ from the virial theorem corresponds to constant mass density throughout the visible galaxy and to orbits that are strongly radial. The resulting ₀^min is about 10 times smaller than ₀ from King's method. But a galaxy with ₀ = ₀^min has a higher global M / L than a galaxy with higher ₀. The minimal total mass required by the virial theorem corresponds to a point mass (black hole) at the center (which cannot be excluded at present, see Pryor 1994). The resulting global (M / L)^min is down by a factor of 3 as compared to M / L derived from King's method. Thus, there is apparently no way to avoid the need for DM in the local dE's (excepting perhaps Sculptor and Fornax). Pryor (1994) concludes that Draco and Ursa Minor, the two most extreme cases, must have central densities larger than 0.1 M pc^-3 and global M / L's larger than 30.

Alternatives to a high DM content call into question the assumption of virial equilibrium, or, at a more fundamental level, the validity of Newtonian gravity. This latter possibility, while it can never be strictly excluded, has become less viable since Gerhard and Spergel (1992b) demonstrated that Milgrom's (1983) Modified Newtonian Dynamics (MOND) does not work for the local dwarfs. However, the first alternative, i.e. that the dwarfs are not in equilibrium but are in a state of tidal dissolution, has proven more persistent. Consider Fig. 5 (right panel). With the exception of Leo II (whose high has yet to be confirmed), the dwarfs show a nice correlation between M / L and galactocentric distance: the closer a dwarf the higher its M / L. The possibility that the closer dwarfs have been tidally heated by the Galaxy, thus mimicking a high M / L, was first explored by Kuhn and Miller (1989). The problem with this scenario is that the time scale of disintegration, in the absence of a dark halo, is rather short ( 10⁸ years), which would make our coexistence with this event very coincidental. Kuhn's (1993) attempt to stretch the survival time of the dwarfs seems unconvincing (Gerhard 1994). Moreover, global tides induce large streaming motions rather than large 's (Piatek and Pryor 1994). On the other hand, dense halo objects (MACHO's) as tidal agents would require unrealistically high perturber masses, while the more promising mechanism of tides from ``halo lumps'' has yet to be explored (Gerhard 1994).

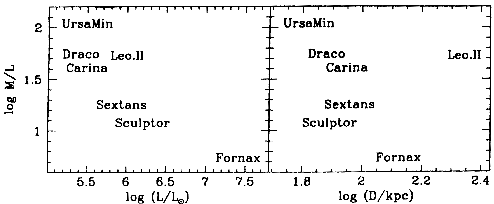
Figure 5. Inferred mass-to-light ratio of the local dwarf elliptical galaxies (Milky Way companions) against luminosity (left panel), and against galactocentric distance (right panel). Taken from Gerhard (1994), based on data compiled by Mateo (1994).

On the observational side, there are hints that tidal effects might be important. Faint extensions have been reported near Ursa Minor (Irwin and Hatzidimitriou 1993) and Sextans (Gould et al. 1992). Gerhard (1994) finds clear signs of streaming motion in Sextans. However, a tidal origin for the high apparent M / L of Draco, Carina, and Ursa Minor appears unlikely.