Annu. Rev. Astron. Astrophys. 1991. 29: 239-274 Copyright © 1991 by Annual Reviews. All rights reserved

2.3.1 ORBITAL STRUCTURE The Hamilton-Jacobi equation separates in ellipsoidal coordinates (173) for the general Stäckel potential. The corresponding mass models have a non-rotating triaxial shape, with an arbitrary short-axis density profile, and arbitrary central axial ratios (81, 90, 197, 198). On projection, the ellipticity of the isophotes generally changes with radius, but they show no twisting (121). All relevant models have cores with non-singular density profiles. The integrals I₂ and I₃ are related to the angular momentum integrals of the axisymmetric and spherical limits (89). The three-dimensional orbital motion is a combination of three one-dimensional motions, each of which is either a libration or an oscillation in one of the three ellipsoidal coordinates. The orbits can be divided into four families: boxes, short-axis tubes, and two families of long-axis tubes (80). These are precisely the four major orbit families found in Schwarzschild's non-rotating triaxial model. Illustrations of the four orbital shapes have been presented by Statler (48, 320). The orbital structure simplifies in limiting cases with more symmetry (Figure 1). Prolate Stäckel models support only inner- and outer long-axis tubes, whereas all orbits are short-axis tubes in oblate separable models.

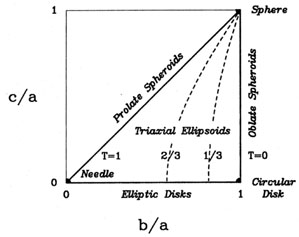
Figure 1. Ellipsoid Land: the plane of all possible axial ratios b / a and c / a for triaxial ellipsoids. The limiting cases with more symmetry are indicated. The dashed lines are curves of constant triaxiality T (see Section 3.4). Oblate spheroids have T = 0, prolate spheroids have T = 1.