

Rapid progress is being made in measuring the cosmological parameters that describe the dynamical evolution and the geometry of the Universe. In essence, this is the first conclusion of this review. The second conclusion is that despite the considerable advances, the accuracy of cosmological parameters is not yet sufficiently high to discriminate amongst, or to rule out with confidence, many existing, competing, world models. We as observers still need to do better. Fortunately, there are a number of opportunities on the horizon that will allow us to do so.
In the context of the general theory of relativity, and assumptions of large-scale homogeneity and isotropy, the dynamical evolution of the Universe is specified by the Friedmann equation
where a (t) is the scale factor, H =
Bounds on several cosmological parameters are summarized in
Figure 1
in a plot of the matter density as a function of the Hubble constant,
following
Carroll, Press &
Turner (1992).
Solid lines represent the
expansion ages for 10, 15, and 20 Gyr in an open (
A number of issues that require knowledge of the cosmological
parameters remain unresolved at present. First is the question of
timescales (H0t0) discussed above;
possibly a related issue is
the observation of red (if they are indeed old) galaxies at high
redshift. Second is the amount of dark matter in the Universe. As
discussed below, many dynamical estimates of the mass over a wide
range of scale sizes are currently favoring values of
Taking the current data at face value, there appears to be a conflict
with the standard Einstein-de Sitter model. In fact, it is precisely
the resolution of these problems that has led to a recent resurgence
of interest in a non-zero value of
Ultimately we will have to defer to measurement as the arbiter amongst
the wide range of cosmological models (and their very different
implications) still being discussed in the literature. A wealth of new
data is becoming available and progress is being made in the
measurement of all of the cosmological parameters discussed below: the
matter density, 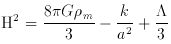
 / a
is the Hubble
parameter (and H0 is the Hubble ``constant'' at the
present epoch),
/ a
is the Hubble
parameter (and H0 is the Hubble ``constant'' at the
present epoch),
 m is the
average mass density, k is a curvature term, and
m is the
average mass density, k is a curvature term, and
 is the cosmological
constant, a term which represents the
energy density of the vacuum. It is common practice to define the
matter density (
is the cosmological
constant, a term which represents the
energy density of the vacuum. It is common practice to define the
matter density ( m =
8
m =
8  G
G  m /
3H02), the vacuum
energy density (
m /
3H02), the vacuum
energy density (
 =
=  /
3H02), and the
curvature term (
/
3H02), and the
curvature term ( k =
-k / a02
H02) so that
k =
-k / a02
H02) so that
 m +
m + 
 = 1 for the case of a flat universe
where k = 0. The simplest case is the Einstein-de Sitter model with
= 1 for the case of a flat universe
where k = 0. The simplest case is the Einstein-de Sitter model with
 m = 1 and
m = 1 and 
 = 0. The dimensionless
product H0t0 (where
t0 is the age of the Universe) is a
function of both
= 0. The dimensionless
product H0t0 (where
t0 is the age of the Universe) is a
function of both  m
and
m
and 
 . In the case
of the Einstein-de Sitter Universe
. In the case
of the Einstein-de Sitter Universe
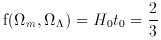
 = 0)
model. The grey box is defined by values of H0 in the
range of 40
to 90 km/sec/Mpc and 0.15 <
= 0)
model. The grey box is defined by values of H0 in the
range of 40
to 90 km/sec/Mpc and 0.15 <  m < 0.4. The solid arrow
denotes the same range in H0 for
m < 0.4. The solid arrow
denotes the same range in H0 for
 m = 1. This plot
illustrates the well-known ``age'' problem;
namely that for an Einstein-de Sitter Universe
(
m = 1. This plot
illustrates the well-known ``age'' problem;
namely that for an Einstein-de Sitter Universe
( = 1,
= 1,  = 0),
H0 must be less than ~ 45
km/sec/Mpc if the ages of globular clusters (t0) are indeed
~ 15 billion years old. This discrepancy is less severe if the
matter density of the Universe is less than the critical density, or
if a non-zero value of the cosmological constant is allowed. For
example, the dashed line indicates an expansion age of 15 Gyr in the
case of a flat (
= 0),
H0 must be less than ~ 45
km/sec/Mpc if the ages of globular clusters (t0) are indeed
~ 15 billion years old. This discrepancy is less severe if the
matter density of the Universe is less than the critical density, or
if a non-zero value of the cosmological constant is allowed. For
example, the dashed line indicates an expansion age of 15 Gyr in the
case of a flat ( m +
m +

 = 1) model for
= 1) model for

 0.
0.
 m
~ 0.25 ± 0.10, lower than the critical Einstein-de Sitter
density. And third is the origin of large-scale structure in the
Universe. Accounting for the observed power spectrum of galaxy
clustering has turned out to be a challenge to the best current
structure formation models.
m
~ 0.25 ± 0.10, lower than the critical Einstein-de Sitter
density. And third is the origin of large-scale structure in the
Universe. Accounting for the observed power spectrum of galaxy
clustering has turned out to be a challenge to the best current
structure formation models.
 (e.g.
Ostriker &
Steinhardt 1995;
Krauss & Turner
1995).
Another means of addressing these issues (e.g.
Bartlett et al. 1995)
requires being in
conflict with essentially all of the current observational
measurements of H0; from purely theoretical
considerations, a very
low value of H0 (
(e.g.
Ostriker &
Steinhardt 1995;
Krauss & Turner
1995).
Another means of addressing these issues (e.g.
Bartlett et al. 1995)
requires being in
conflict with essentially all of the current observational
measurements of H0; from purely theoretical
considerations, a very
low value of H0 ( 30) could also resolve these issues.
30) could also resolve these issues.
 m,
the vacuum energy density,
m,
the vacuum energy density, 
 , the expansion rate
H0, and age of the oldest
stars t0. The central, critical issues now are (and in fact
have always been) testing for and eliminating sources of significant
systematic error.
, the expansion rate
H0, and age of the oldest
stars t0. The central, critical issues now are (and in fact
have always been) testing for and eliminating sources of significant
systematic error.