One of the most exciting future developments with respect to the accurate measurement of cosmological parameters will be the opportunity to measure anisotropies in the cosmic microwave background to high precision. Planned balloon-born experiments (e.g., MAX, MAXIMA, and Boomerang) will shortly measure the position of the first acoustic peak in the cosmic background anisotropy spectrum. Even more promising are future satellite experiments (e.g., MAP to be launched by NASA in 2000, and the European COBRAS/SAMBA mission, now renamed the PLANCK Surveyor mission, currently planned to be launched in 2005).
The underlying physics governing the shape of the anisotropy spectrum
is that describing the interaction of a very tightly coupled fluid
composed of electrons and photons before (re)combination (e.g.,
Hu & White 1996;
Sunyaev &
Zel'dovich 1970).
It is elegant, very
simple in principle, and offers extraordinary promise for measuring
cosmological parameters; (e.g., H0, 
0, and
the baryon density b
to precisions of 1% or better:
Bond, Efstathiou &
Tegmark 1997).
The final accuracies will of course (again) depend on how well various systematic errors can be controlled or eliminated. The major uncertainties will be determined by how well foreground sources can be subtracted, and probably to a lesser extent, by calibration and instrumental uncertainties. (PLANCK will provide a cross check of the MAP calibration.) Potentially the greatest problem is the fact that extracting cosmological parameters requires a specific model for the fluctuation spectrum. Currently the estimates of the precisions (i.e., without systematic effects included) are based on models in which the primordial fluctuations are Gaussian and adiabatic, and for which there is no preferred scale. A very different anisotropy power spectrum shape is predicted for defect theories (Turok 1996), but these calculations are more difficult and have not yet reached the same level of predictive power. Important additional constraints will come from polarization measurements e.g., Zaldarriaga, Spergel & Seljak 1997; Kamionkowski et al. 1997). The polarization data will provide a means of breaking some of the degeneracies amongst the cosmological parameters that are present in the temperature data alone. Furthermore, they are sensitive to the presence of a tensor (gravity wave) contribution, and hence will allow a very sensitive test of inflationary models.
Figure 4 shows a plot of the predicted angular
power spectrum for
cosmic microwave background (CMB) anisotropies reproduced from
Hu, Sugiyama, &
Silk (1997).
The position of the first acoustic peak is
very sensitive to the value of 0, and, as noted by these
authors, the spacing between the acoustic peaks in the power spectrum
appears to provide a fairly robust measure of 0. The
accurate determination of other cosmological parameters will require
the measurement of peaks at smaller (arcminute) angular scales. In
general, the ratio of the first to the third peaks is sensitive to the
value of value of H0 (e.g.,
Hu & White 1996).
Excellent sky
coverage is critical to these efforts in order to reduce the sampling
variance.
|
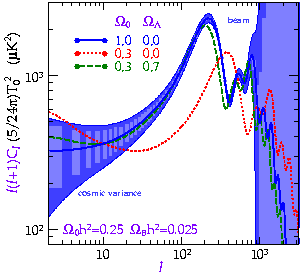
Figure 4. The angular power spectrum
of cosmic
microwave background anisotropies assuming adiabatic, nearly
scale-invariant models for a range of values of |
Can the cosmological parameters be measured to precisions of 
1% with currently planned experiments as advertised above? I
believe that both MAP and PLANCK are likely to revolutionize
our understanding of cosmology. Observation of a Gaussian, adiabatic
fluctuation spectrum would be a stunning confirmation of the
``standard'' cosmology. However, equally fundamental would be the
case where the observed anisotropy spectrum resembles nothing like
those for any of the various current theoretical predictions. In the
former case, if foreground effects can be accounted for, then
measurement of the cosmological parameters to these levels of
precision will eventually follow. However, in the latter case, at
least until the origin of the spectrum could be predicted from first
principles, all bets would be off for the determination of
cosmological parameters.
Can the foreground subtraction be accounted for accurately enough to yield final accuracies of 1% (or better)? There will be foreground contributions due to faint, diffuse Galactic emission. MAP will have 5 frequency bands ranging from 22 to 90 GHz allowing both the spectral and spatial distribution of the Galactic foreground to be measured. PLANCK will have 9 frequency channels from 30 GHz to 900 GHz. However, there are many sources of foregrounds whose subtraction is critical; perhaps the greatest unknown is the potential contribution from GHz radio sources, many of which could potentially also be variable sources. Deep 90 GHz radio surveys from the ground might address the question of how serious an issue such sources could be (Spergel, private communication). Although MAP will cover any given region of the sky several times, the signal-to-noise for an individual image will be insufficient to detect any but the brightest sources. In addition there will be foreground contributions due to diffuse emission from external galaxies, dust within galaxies, and bright infrared luminous galaxies. Until these experiments are completed, it will be difficult to assess whether these systematic uncertainties are likely to be small relative to the quoted formal uncertainties.
(
). The position of the first
acoustic peak is predicted to be at l
~ 220