The recent success in the measurement of cosmological parameters can be attributed to a number of factors: an abundance of new observations, new approaches, and developments in detector technology (with a corresponding increase in the precision of the data). Given these advances, it is tempting to conclude that we have now entered an era of precision cosmology. Of course, whether this is indeed the case depends completely on the extent to which systematic measurement errors have been minimized or eliminated. In this context, it is interesting to view the measurement of cosmological parameters from a historical perspective as described briefly in the next section below. The present review concentrates primarily on results of the past couple of years, following on from a review on a similar topic given at the Texas Symposium in December, 1996 (Freedman 1997a).
The cosmological parameters discussed in this review are the
following: the matter density 
m = 8
G
m /
3H02,
the Hubble parameter H = 
/ a, (where a is the scale
factor and H0, the Hubble constant, is the value at
the current epoch), the vacuum energy density 
= /
3H02, and the age of the universe,
t0. In Big Bang cosmology,
the Friedmann equation relates the density, geometry and evolution of
the universe: H2 = 8 G m / 3 - k / a2 +
/ 3, where the average mass
density is specified by
m. The
curvature term is specified by k = -k / a02
H02, and for the case of a flat universe
(k = 0),
m + = 1. A lower limit to the age,
t0, can be determined by dating the oldest objects in
the Universe.
Or, alternatively, given an independent knowledge of the other
cosmological parameters (H0, m, ,
and k), a dynamical
age of the Universe can also be
determined by integrating the Friedmann equation.
Before moving on to describe recent developments, it is interesting to
view how the values for these parameters have changed over time. In
Figures 1a-b and
2a-b, estimates of H0, m, 
, and
t0 are shown as a function of time. The historical discussion
below is not intended to be comprehensive, but rather to outline the
general trends as shown in Figures 1 and
2. Each of the figures is discussed in turn.
|
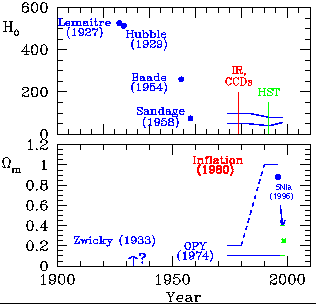
Figure 1a-b. The trend with time for
measurements of H0 and |
|
Figure 2a-b. The trend with time for
|
H0 (Figure 1a): Over the last half century, the value of H0, the expansion rate of the Universe, has remained a well-known source of disagreement (for historical reviews see, for example, van den Bergh 1997; Rowan-Robinson 1985). After Baade (1954) recalibrated the Cepheid distance scale, and Sandage (1958) recognized that the brightest stars in galaxies were ionized HII regions, the Hubble constant decreased from its original value of over 500, and fell into the well-known range of a factor of two, loosely constrained, as shown by the schematic lines drawn in Figure 1a, between about 50 and 100 km/sec/Mpc. As indicated in the figure and discussed further below, recent improvements have come about as a result of new instrumentation and the availability of the Hubble Space Telescope (HST); in addition, several new methods for measuring distances to galaxies have been developed (see also Livio, Donahue & Panagia 1997; Freedman 1997b). Recently, there has been some convergence in the value of H0. Although decreasing, the dominant errors in H0 remain systematic in nature.
m
(Figure 1b):
Zwicky (1933)
provided evidence that
there was possibly 10-100 times more mass in the Coma cluster than
contributed by the luminous matter in galaxies. However, it was not
until the 1970's that the existence of dark matter began to be taken
more seriously. At that time, evidence began to mount that showed
rotation curves did not fall off with radius (e.g.,
Rogstad & Shostak 1972;
Rubin et al. 1978; and
Bosma 1981)
and that the
dynamical mass was increasing with scale from that of individual
galaxies up through groups of galaxies (e.g.,
Ostriker, Peebles &
Yahil 1974).
A comprehensive historical review of the dark matter issue can be found in
Trimble (1987).
By the 1970's, the evidence was
consistent with a total matter density of ~ 10-20% of a critical
density, ( = 1) universe. With
the development of inflation in the early 1980's
(Guth 1981),
tremendous effort was aimed at
discovering both the nature and the amount of dark matter. In the
early 1990's (see, for example, the review by
Dekel, Burstein &
White 1997),
a number of studies indicated that we live in a critical
density universe, and the first results for high redshift supernovae
(Perlmutter 1997)
were also consistent with a high matter density. As
described below, however, the new supernovae results, and a wide range
of other studies are consistent (once again) with a lower matter
density of m ~ 0.2
to 0.3. The overall trends in
m with time are
shown in Figure 1b. The solid and dotted
lines represent approximate upper and lower bounds only.
(Figure 2a): The
reader is referred to excellent overviews of the cosmological constant by
Weinberg (1989) and
Carroll, Press &
Turner (1992).
Enthusiasm for a non-zero value of
has come and gone several times over this century. For fun, I have
plotted (in arbitrary units), the ``market value'' for shares of
in
Figure 2a. Here it can be
seen that the market for
has been quite volatile over
time. Shares for were high when
Einstein (1917)
first introduced this cosmological
constant in an attempt to allow for a stable universe; subsequent
work, for example, by
Friedmann (1922),
followed by the discovery of
the expansion of the Universe by Edwin Hubble, led to the crash of
(along with the rest of the
stock market) in 1929!
The value of H0 measured by
Hubble (1929)
implied a dynamical age
for the Universe of only ~ 2 billion years. This age was younger
than the geological dating estimates for the age of the Earth, placed
then at about 3.5 billion years. This discrepancy led to an ``age
crisis'', and a renewal of interest in , that was eventually
solved by Baade's recalibration of the distance scale in 1954. A
brief period of activity occurred in the market with the observation by
Petrosian et al. (1967),
of an apparent peak at
z ~ 2 in the quasar distribution. However, as more quasars were
observed, this feature also disappeared.
In general, consumers have tended to been wary of stock in
due to the difficulties of explaining the current limits in conflict
by 120 orders of magnitude with the predictions of the standard model
of particle physics (e.g.,
Weinberg 1989).
However, recently,
as Figure 2a shows, the low observed matter
density, the recurring
conflict in ages between some values of H0 and
globular cluster
ages, and the observed large-scale distribution of galaxies have
motivated a renewed interest in (e.g.,
Krauss & Turner 1995;
Ostriker & Steinhardt
1995).
Just as for other
commodities, the consumer may need to be concerned about how inflation
is driving the market. It is probably too early to say if the bull
market of the 1990's is over - this is an area where, as in the
world of the stock market, the experts disagree!
t0 (Figure 2b): In the 1950's, the first applications of stellar evolution models to determine ages for globular clusters resulted in ages somewhat older than the age of the Earth; these estimates climbed considerably to about 26 billion years in the early 1960's as illustrated in Figure 2b. Much of this increase resulted from a change in the adopted helium abundance (see the historical review by Demarque et al. 1991). As described by Demarque et al. (and references therein), the value of 5 billion years obtained by Sandage in 1953 assumed a helium abundance of Y = 0.4, whereas the value of 26 billion years obtained by Sandage in 1962 was based on an adopted value of Y = 0.1. The age estimates began to stabilize once it was recognized that the helium abundance for globular clusters was closer to that of the Sun (Y ~ 0.25). The ages of globular clusters have remained at approximately 15-16 billion years (bracketed loosely by the bounds shown schematically in the figure) for some time; only recently, with the new results from the Hipparcos satellite (plus new opacities) have the ages again dropped systematically. These new results are discussed further below.
These cartoons illustrate a couple of simple and obvious points. Ultimately, values of cosmological parameters will not be determined by market value or popular enthusiasm; they must come from accurate experiments. But as also indicated in these plots, such measurements are difficult, they are dominated by systematic uncertainties, and so require a very high level of testing, independent measurements and scrutiny, before we can know with confidence if convergence (if any) is real.