


4.3 The Extragalactic Distance Scale
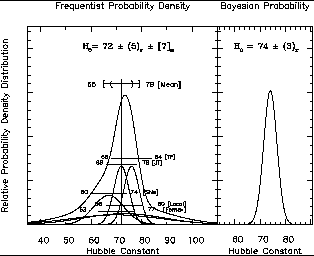
The launch of the Hubble Space Telescope (HST) in 1990 has provided the opportunity to undertake a major program to calibrate the extragalactic distance scale. The resolution of HST is an order of magnitude higher than can be generally obtained through the Earth's atmosphere, and moreover it is stable; as a result, the volume of space made accessible by HST increased by 3 orders of magnitude. The HST Key Project on the extragalactic distance scale was designed to measure the Hubble constant to an accuracy of ± 10% rms (Freedman et al. 1994; Mould et al. 1995; Kennicutt et al. 1995). Since the dominant sources of error are systematic in nature, the approach we have taken in the Key Project is to measure H0 by intercomparing several different methods. This approach allows us to assess and quantify explicitly the systematic errors. The HST Key Project will be completed in 1999; since new results will be available shortly, this discussion will be kept very brief. Results based on half of the available data yield H0 = 72 ± 5 ± (random) 7 (systematic) km/sec/Mpc (Madore et al. 1998, 1999; Freedman et al. 1998; Mould et al. 1997). In Figure 4, the results for various H0 methods are combined using both a Frequentist and a Bayesian approach (from Madore et al.).
|
Figure 4. Plot of various H0 determinations and the adopted values from Madore et al. (1998). In the left panel, each value of H0 and its statistical uncertainty is represented by a Gaussian of unit area (linked dotted line) centered on its determined value and having a dispersion equal to the quoted random error. Superposed immediately above each Gaussian is a horizontal bar representing the one sigma limits of the calculated systematic errors derived for that determination. The adopted average value and its probability distribution function (continuous solid line) is the arithmetic sum of the individual Gaussians. This Frequentist representation treats each determination as independent, and assumes no a priori reason to prefer one solution over another. A Bayesian representation of the products of the various probability density distributions is shown in the right panel. Because of the close proximity and strong overlap in the various independent solutions the Bayesian estimator is very similar to, while more sharply defined than, the Frequentist solution. |
The largest remaining sources of uncertainty in the extragalactic distance route to H0 can be traced to uncertainty in the distance to the Large Magellanic Cloud (the galaxy which provides the fiducial comparison for more distant galaxies), and to the potential effects of differing amounts of elements heavier than helium (or metallicity). The importance of the latter effect has been difficult to establish. The recently-installed infrared (NICMOS) camera on HST is being used to address this, and may help to resolve the issue shortly.
|
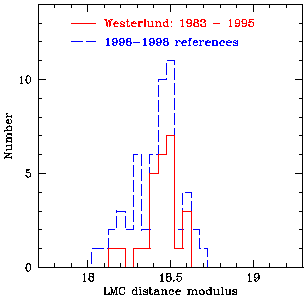
Figure 5. A histogram of distance moduli determinations for the Large Magellanic cloud. Values prior to 1996 are from a published compilation by Westerlund (1997). |
A histogram of the distribution of distances to the LMC from the literature is shown in Figure 5. The distances in this histogram are based on Cepheids, RR Lyraes, SN 1987A, red giants, the ``red clump'', and long-period variables. Values prior to 1996 come from the published compilation of Westerlund (1997), but only the latest revision published by a given author is plotted for a given data set. Despite decades of effort in measuring the distance to this nearby neighboring galaxy, and the number of independent methods available, the dispersion in measured distance modulus remains very high. Moreover, the distribution is not Gaussian. There has been much recent activity on the red clump which contributes many of the values around 18.3 mag, and gives rise to the bimodal nature of the distribution. There is as yet no understanding of why there is a systematic difference between the Cepheid and the red clump distance scale. This histogram illustrates that the uncertainty in the distance to the LMC is still large. Without assuming that the distribution is Gaussian, the 95% confidence limits are ± 0.28 mag, and the 68% confidence limits amount to ± 0.13 mag or 7% in distance. Unfortunately, the distance to the LMC remains as one of the largest systematic uncertainties in the current extragalactic distance scale.