7. DISCUSSION AND SUMMARY

In the past year, a radical shift has begun to occur. Until recently, a majority of the theoretical community viewed the (standard) Einstein-de Sitter model (₀ = 1, = 0) as the most likely case (with h = 0.5, t = 13 Gyr). With accumulating evidence for a low matter density, difficulty in fitting the galaxy power spectrum with the standard model, the conflict in ages for the Einstein-de Sitter case, and now, most recently, the evidence from type Ia supernovae for an accelerating universe, a new ``standard'' model is emerging, a model with _m ~ 0.3, ~ 0.7, h = 0.65, and t = 13 Gyr. This model preserves a flat universe and is still consistent with inflation.

In Figure 7, the bounds on several cosmological parameters are summarized in a plot of the matter density as a function of the Hubble constant. What do these current limits on cosmological parameters imply about the contribution of non-baryonic dark matter to the total matter density? As can be seen from the figure, for H₀ = 70 km/sec/Mpc, current limits to the deuterium abundance (Burles & Tytler 1998; Hogan 1998) yield baryon densities in the range of _b = 0.02 to 0.04, or 2-4% of the critical density. Given current estimates of the matter density (_m ~ 0.3), non-baryonic matter would thus contribute just over 25% of the total energy density needed for a flat, = 1 universe.

Figure 7. Plot of m versus H0 showing current observational limits on cosmological parameters. The shaded box is defined by values of H0 in the range of 40 to 90 km/sec/Mpc and 0.15 < m < 0.4. The thick solid lines denote expansion ages for an open ( = 0) Universe for 10, 15, and 20 Gyr and the thick dashed lines denote expansion ages in the case of a flat ( m + = 1) Universe. The light dashed lines denote current limits for b based on low and high values for the deuterium to-hydrogen ratio.

One might ask, is non-baryonic dark matter still required if is non-zero? Allowance for 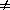0 does not provide the missing energy to simultaneously yield = 1, while doing away with the necessity of non-baryonic dark matter, at least for the current limits from Big Bang nucleosynthesis. As can be seen from Figure 7, for the current deuterium limits, having all baryonic mass plus would require both H₀ ~ 30 km/sec/Mpc and an age for the Universe of ~ 30 Gyr. These H₀ and age values are outside the range of currently measured values for both of these parameters. Although it might be appealing to do away simultaneously with one type of unknown (non-baryonic dark matter) while introducing another parameter (), a non-zero value for the cosmological parameter does not remove the requirement for non-baryonic dark matter.

The question of the nature of dark matter (or energy) remains with us. In this sense, the situation has not changed very much over the past few decades, although the motivation for requiring a critical-density universe has evolved from considerations of fine-tuning and causal arguments to the development of inflation. But searches for dark matter since the 1970's have not uncovered sufficient matter to result in a critical-density universe. This year has offered exciting new (and therefore still tentative) results that a non-zero value of the cosmological constant, or perhaps an evolving scalar field like quintessence (Steinhardt, this volume; Steinhardt & Caldwell 1998) could provide the missing energy to result in a critical-density universe. Still, the nature of the dark matter, whether it contributes 25% or 95% of the total energy density, is unknown, and remains as one of the most fundamental unsolved problems in cosmology.

The progress in measuring cosmological parameters has been impressive; still, however, the accurate measurement of cosmological parameters remains a challenging task. It is therefore encouraging to note the wealth of new data that will appear over the next few years, covering very diverse areas of parameter space. For example, measurement of CMB anisotropies, (from balloons and space with MAP, and Planck), the Sloan Digital Sky Survey, Hubble Space Telescope, Chandra X-ray Observatory, radio interferometry, gravitational lensing studies, weakly interacting massive particle (WIMP) cryogenic detectors, neutrino experiments, the Large Hadron Collider (LHC), and a host of others, inspire optimism that the noose on cosmological parameters is indeed tightening. At the very least, the next few years should continue to be interesting!

Acknowledgments

It is a great pleasure to thank the organizers of this Nobel Symposium for a particularly enjoyable and stimulating conference, and for their immense hospitality. I also thank Brad Gibson for his help with the LMC distance literature search.