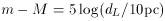In these lectures I shall discuss the status of the determination
of the three cosmological parameters
which enter the Einstein equation and govern geometry
and evolution of space-time of the Universe:
the Hubble constant H0,
the mass density parameter 
and
the cosmological constant
.
Among the three parameters, the Hubble constant is the dimensionfull quantity which sets the basic size and age of the Universe. The perennial effort to determine H0 dates back to Hubble (1925) and has a long history of disconcordance. Recent progress has done much to resolve the long-standing discrepancy concerning the extragalactic distance scale, but there are some newly revealed uncertainties in the distance scale within the Milky Way. The emphasis in this lecture is on discussion of these uncertainties.
The mass density parameter directly determines the formation of
cosmic structure. So, as our understanding of the cosmic structure
formation is tightened, we should have a convergence of the
parameter. An important test
is to examine whether the
parameter extracted from
cosmic structure formation agrees with the value estimated in more
direct ways. This gives an essential verification for the theory of
structure formation.
The third important parameter in the Friedmann universe is the cosmological
constant 
. We now have some
evidence for a
non-zero which, if
confirmed, would have most profound implications for
fundamental physics. This lecture will focus on
the strength of this `evidence'.
We take the normalisation
for the flat curvature, where
instead of the distance dL. For conciseness, we shall
omit the units
for the Hubble constant, (km s-1 Mpc-1).
After the Summer Institute there appeared several important papers on
the distance scale. I try to incorporate these results in this article.
=
/
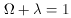
3H20 with
the constant entering in the
Einstein equation.
The case with = 1 and
= 0 is referred to as
the Einstein-de Sitter (EdS) universe.
We often use distance modulus
