


2.2. Extragalactic Distance Scale
The measurement of cosmological distances traditionally employs distance ladders (see Weinberg 1972). The most traditional ladders are shown in TABLE 2. The listings written in italic indicate new methods which circumvent intermediate rungs. The most important milestone of the ladder is LMC at 50kpc (m - M = 18.5). A distance indicator of particular historical importance (Hubble 1925) is the Cepheid period-luminosity (PL) relation, which is given a great confidence, but we note that it requires a few rungs of ladders to calibrate its zero point.
| Method | Distance range | typical targets |
| Population I stars | ||
| trigonometric or kinematic methods (ground) | < 50 pc | Hyades, nearby dwarfs |
| main sequence fitting (FG stars) Pop. I | < 200pc | Pleiades |
| trigonometric method (Hipparcos) | < 500pc | nearby open clusters |
| main sequence fitting (B stars) | 40pc-10kpc | open clusters |
| Cepheids [Population I] (ground) | 1kpc-3Mpc | LMC, M31, M81 |
| Cepheids [Population I](HST) | < 30Mpc | Virgo included |
| secondary (extragalactic) indicators | 700kpc-100Mpc | |
| Population II stars | ||
| trigonometric method (Hipparcos) | < 500pc | nearby subdwarfs |
| subdwarf main sequence fitting | 100pc-10kpc | global clusters |
| cluster RR Lyr | 5kpc-100kpc | LMC, age determinations |
Prior to the HST work there were only 4-5 galaxies with Cepheid distances which could be used to calibrate secondary indicators. The reach of the ground-based Cepheid measurement is about 3 Mpc, which means that one cannot increase the number of calibrating galaxies from the ground. Pierce et al. (1994) could finally measure Cepheids in NGC 4571 in the Virgo cluster at 15 Mpc, but only with the best seeing conditions and difficult observations. The refurbishment of HST achieved a sufficient power to resolve Cepheids at the Virgo cluster (Freedman et al. 1994). Now 28 nearby spiral galaxies within 25 Mpc are given distances measured using the Cepheid PL relation (Ferrarese et al. 1999b). A typical random error is 4-5% (0.08-0.10 mag), and the systematic error (from photometry) is 5% (0.1 mag) excluding the uncertainty of the LMC distance, to which the HST-Key Project(KP) group assigns 6.5% error (0.13 mag). The prime use of these galaxies is to calibrate secondary distance indicators which penetrate into a sufficient depth that perturbations in the Hubble flow are small enough compared with the flow itself.
Cepheids are Population I stars, so reside only in spiral galaxies.
The calibration is therefore direct for TF and some SNeIa. For early
type galaxies (fundamental plane or Dn -
 , and SBF) the
calibration is not very tight;
one must either use some groups where both
early and late galaxies coexist, or regard the bulges of spiral galaxies
as belonging to the same class as early galaxies and avoid contaminations
from discs.
Additional observations have been made for the galaxies that host
SNeIa
(Saha et al. 1999).
The results are summarised in TABLE 3. We include
a few earlier SNIa results which employ a partial list of Cepheid calibrators.
, and SBF) the
calibration is not very tight;
one must either use some groups where both
early and late galaxies coexist, or regard the bulges of spiral galaxies
as belonging to the same class as early galaxies and avoid contaminations
from discs.
Additional observations have been made for the galaxies that host
SNeIa
(Saha et al. 1999).
The results are summarised in TABLE 3. We include
a few earlier SNIa results which employ a partial list of Cepheid calibrators.
| Secondary indicators | Refs | Hubble constant |
| Tully-Fisher | HST-KP (Sakai et al. 1999) | 71 ± 4 ± 7 |
| Fundamental Plane | HST-KP (Kelson et al. 1999) | 78 ± 8 ± 10 |
| SBF | HST-KP (Ferrarese et al. 1999a) | 69 ± 4 ± 6 |
| SBF | Tonry et al. (1999) | 77 ± 4 ± 7 |
| SNeIa | Riess et al. (1995) | 67 ± 7 |
| SNeIa | Hamuy et al. (1996b) | 63 ± 3 ± 3 |
| SNeIa | Jha et al. (1999) | 64.4+5.6-5.1 |
| SNeIa | Suntzeff et al. (1999) | 65.6 ± 1.8 |
| SNeIa | HST-KP (Gibson et al. 1999) | 68 ± 2 ± 5 |
| SNeIa | Saha et al. (1999) | 60 ± 2 |
| Summary (see text) | (64-78) ± 7 | |
We accentuate the results with the two methods,
SBF and SNeIa, in particular to those we underlined in the table.
A cross correlation analysis showed that the relative
distances agree well between SBF and others, including the Cepheid
(Tonry et al. 1997;
Freedman et
al. 1997),
and that it is probably the best secondary indicator presently
available together with SNeIa; Also important is that
there are now 300 galaxies measured with SBF, which are essential to
make corrections for peculiar velocity flows for their
 4000
km s-1 sample
(Tonry et al. 1999).
(PNLF is an indicator of
comparable quality, but it requires more expensive observations so that
applications are rather limited; see
Jacoby et al. 1996
for the recent work.)
The final value of Tonry et al. from their I band survey
is H0 = 77 ± 8, in which ± 4
is allotted to uncertainties in the flow model and another ± 4
to SBF calibration procedure in addition to the error of the Cepheid
distance ± 6 (a quadrature sum is taken).
There are a several other pieces of the SBF work to determine
H0, which generally
result in H0 = 70-90 (e.g.,
Thomsen et al. 1997
using HST;
Jensen et al. 1999
with K band; see a review by
Blakeslee et
al. 1999).
The new calibration made by the HST-KP group
(Ferrarese et
al. 1999a)
would decrease H0 only by
2%. The difference in the final H0 between Tonry et al. and
Ferrarese et al. comes from using different targets (the latter authors use
only 4 clusters) and flow models.
4000
km s-1 sample
(Tonry et al. 1999).
(PNLF is an indicator of
comparable quality, but it requires more expensive observations so that
applications are rather limited; see
Jacoby et al. 1996
for the recent work.)
The final value of Tonry et al. from their I band survey
is H0 = 77 ± 8, in which ± 4
is allotted to uncertainties in the flow model and another ± 4
to SBF calibration procedure in addition to the error of the Cepheid
distance ± 6 (a quadrature sum is taken).
There are a several other pieces of the SBF work to determine
H0, which generally
result in H0 = 70-90 (e.g.,
Thomsen et al. 1997
using HST;
Jensen et al. 1999
with K band; see a review by
Blakeslee et
al. 1999).
The new calibration made by the HST-KP group
(Ferrarese et
al. 1999a)
would decrease H0 only by
2%. The difference in the final H0 between Tonry et al. and
Ferrarese et al. comes from using different targets (the latter authors use
only 4 clusters) and flow models.
It is impressive that analyses of SNeIa Hubble diagram give virtually the same answer, even though the samples are all derived primarily from the Calán-Tololo sample of Hamuy et al. (1996b). A smaller H0 of Saha et al. (1997) basically reflects the absence of the the luminosity-decline rate correction, which pushes up H0 by 10%. The other notable difference is a slightly higher value of HST-KP (Gibson et al. 1999), who made a reanalysis for all Cepheid observations performed by other groups and showed that their distances (to SN host galaxies) are all farther than would be derived from the HST-KP procedure. The average offset is as large as 0.16 mag (8%). This correction applies to all results other than HST-KP should we keep uniformity of the Cepheid data reduction. This is important especially when one compares the SN results with those from other secondary distance indicators, since the calibrations for the latter exclusively use HST-KP photometry. Taking the luminosity-decline rate correlation to be real and adopting Cepheid distance from the HST-KP data reduction, I adopt H0 = 68 from SNeIa.
We present two plots in Figure 1,
(a) the estimates of maximum brightness of different authors and
(b) the decline rate
 m15, the
amount of the decrease in brightness over
15 days following maximum light,
both as a function of metallicity [O/H]. The second plot shows how
metallicity effects are absorbed by the
MVmax -
m15, the
amount of the decrease in brightness over
15 days following maximum light,
both as a function of metallicity [O/H]. The second plot shows how
metallicity effects are absorbed by the
MVmax -
 m15
relation and the first proves that there is little metallicity dependence
in the corrected maximum brightness, though some scatter is seen among
authors.
m15
relation and the first proves that there is little metallicity dependence
in the corrected maximum brightness, though some scatter is seen among
authors.
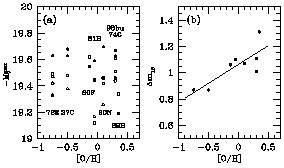
|
Figure 1. (a) Maximum brightness of SNeIa
(in the V band)
adopted by different authors
(see TABLE 3) as a function of [O/H] of host galaxies:
solid circles,
Gibson et
al. (1999);
solid triangles, Suntzeff et al. 1999; open circles,
Jha et al. (1999);
open triangles,
Hamuy et
al. (1996b);
open square,
Saha et
al. (1999).
Note that Saha et al.'s calibration is not necessarily brighter, which is
mainly due to a different treatment of extiction.
(b) The decline rate
|
Leaving out the uncertainty of the Cepheid distance, H0 from
Tonry et al.'s SBF is 77 ± 6, and that from SNeIa (HST-KP) is
68 ± 4. The difference is 13%, and the two values overlap at
H0 = 71. Allowing for individual two sigma errors, the
overlap is in a range of H0 = 65-76. An
additional uncertainty is 6% error
( H0 = ± 4.5)
from the Cepheid distance which is common to both, still excluding the
uncertainty of the LMC distance. We may summarise H0 =
71 ± 7 or 64-78
as our current standard, provided that LMC is at 50 kpc.
All numbers in the table are within this range,
except for the central value of
Saha et al (1997).
H0 = ± 4.5)
from the Cepheid distance which is common to both, still excluding the
uncertainty of the LMC distance. We may summarise H0 =
71 ± 7 or 64-78
as our current standard, provided that LMC is at 50 kpc.
All numbers in the table are within this range,
except for the central value of
Saha et al (1997).
In passing, let us note that H0 = 75 ± 15 (Freedman et al. 1997) obtained directly from the Cepheid galaxy sample agrees with the global value, implying that peculiar velocities are not so large even in a 10-20 Mpc region.
This convergence is a great achievement, but keep in mind that the SNeIa results are still lower than those from other secondary indicators (1) by 10%. There are additional problems. First, all these analyses are based on a LMC distance modulus of m - M = 18.50 (Feast & Walker 1987; Madore & Freedman 1991), which has recently been cast into doubt. In addition, metallicity effects could lead to systematic errors. Finally, should we derive the Hubble constant with the error of 10%, the problem of dust extinction could be an issue, and it is potentially coupled with the metallicity. We now consider these issues in greater detail.
1 A remark is given to
the TF distance. While Sakai et al. (HST-KP) derived
H0 = 71 ± 8 using
Giovanelli et al.'s
(1997)
cluster sample, Tammann and collaborators
(Tammann 1999;
Sandage & Tammann
1997)
insist on a low value H0 = 53-56.
Their cluster result
(Federspiel et
al. 1998)
neglects the depth effect of the Virgo cluster: contrary to ellipticals,
spiral galaxies are distributed elongating along the line of sight
(Yasuda et
al. 1996).
Hence identifying
the centre of gravity of the spiral galaxy distribution
with the true core leads to an offset. In fact the presence of
substructure behind the Virgo core is confirmed with the
Cepheid for NGC4649.
Tammann et al.'s field result
comes from the allocation of an unusually large dispersion
to the TF relation,
which largely amplifies the Malmquist bias.
Tully (1999)
obtained H0 = 82 ± 16
(Tully et al. 1998).
Back.