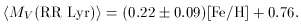2.3.5. RR Lyr Problems
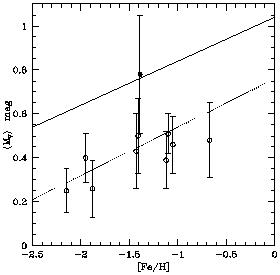
In the first approximation the luminosity of RR Lyr is constant, but in reality it depends on metallicity. The dependence is usually expressed as
Much effort has been invested to determine a and b.
The problem is again how to
estimate the distance to RR Lyr. Unlike the case with Cepheids,
there are no unique ladders for the calibration, and a variety of
methods have been used, of which the best known is the Baade-Wesselink method.
The calibration from the ground may be summarised as
With this calibration we are led to the LMC distance of
m - M
The Hipparcos catalogue contains a number of field subdwarfs with
parallax. This makes a ladder available to calibrate RR Lyr
in globular clusters.
Gratton et al. (1997)
and Reid (1997)
carried out this subdwarf fitting. Gratton et al. gave
Their data are plotted in Figure 2, together
with (4) and (5).
Reid's result is also consistent.
This zero point, being brighter by 0.3 mag (at [Fe/H] = -1.8)
compared to (4), would bring the LMC distance to m - M = 18.5-18.6.
There are a few analyses using the statistical parallax
for field RR Lyr in the Hipparcos catalogue.
Fernley et al. (1998)
reported that their
halo RR Lyr lie almost exactly on the curve of (4), rather than (5),
and concluded a confirmation of the ground-based calibration.
This is also endorsed by an analysis of
Gould & Popowski
(1998).
The distance to eponymous RR Lyr was measured by
Hipparcos.
We see (Fig. 2) that RR Lyr itself does not fall
on (5), but almost
exactly on (4), although the error is fairly large.
The uncertainties by 0.3 mag in the RR Lyr calibration
translate to the LMC distance modulus 18.25-18.55.
Figure 2. Calibrations of RR Lyr. The open
points are taken from
Gratton et
al. (1997)
with the dotted line indicating (5). The solid line is the
ground-based calibration (4). The solid point denotes the eponymous RR Lyr
measured by the Hipparcos satellite.
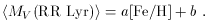
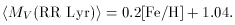
 18.3, as we saw
in TABLE 1 above.
18.3, as we saw
in TABLE 1 above.