


2.6.2. Gravitational Lensing Time Delay
When quasar image is split into two or more by gravitational lensing, we expect the time delay among images, arising from different path lengths and gravitational potentials among image positions. The time delay between images A and B takes the form
where
The first case where H0 is derived is with the
0957+561 lens system. The deflector
is complicated by the fact that a giant elliptical galaxy is embedded into a
cluster.
Falco, Gorenstein
& Shapiro (1991)
noted an ambiguity associated with a galaxy mass - cluster mass separation,
which does not change any observed lens properties but affects the
derived Hubble constant. One way to resolve this degeneracy is to use the
velocity dispersion of the central galaxy
(Falco et al. 1991;
Grogin & Narayan
1996).
Kundic et
al. (1997b),
having resolved a
long-standing uncertainty about the time delay, obtained
H0 = 64 ± 13 employing the Grogin-Narayan model.
Tonry & Franx (1999)
revised it to 71 ± 7 with their new velocity dispersion
measurement near the central galaxy. More recently,
Bernstein &
Fischer (1999)
searched a wider
variety of models, also using weak lensing information to constrain the
mass surface density of the cluster component, and concluded
H0 = 77+29-24,
the large error representing uncertainties associated with the choice
of models.
The second example, PG1115+080,
is again an unfortunate case. The deflector
is elliptical galaxy embedded in a Hickson-type compact group of galaxies
(Kundic et
al. 1997a).
Keeton & Kochanek
(1997)
and Courbin et
al. (1997)
derived (51-53) ± 15
from the time delay measured by
Schechter et
al. (1997).
Impey et al. (1998)
examined the dependence of the derived H0 on the
assumption for the dark matter distribution, and found it to vary from
44 ± 4 (corresponding to M/L linearly increasing with the distance)
to 65 ± 5 (when M/L is constant over a large scale).
The latter situation may sound strange, but it seems not too unusual
for elliptical galaxies, a typical example being seen in NGC5128
(Peng et al. 1998).
Recently, time delays have been measured for three more lenses, B0218+357,
B1608+656 and PKS1830-211. B0218+357 is a rather clean,
isolated spiral galaxy lens, and
Biggs et al. (1999)
derived H0 = 69+13-19
(the central value will be 74 if
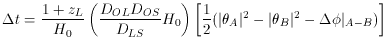
 is the angular
difference between the source and image,
is the angular
difference between the source and image,

 is the difference in the potential
and DIJ is the angular diameter distances.
The time delay is observable if the source is variable,
and can be used to infer H0
(Refsdal 1964).
Crucial in this argument is
a proper modelling of the mass distribution of the deflector.
The DD/D factor depends on
is the difference in the potential
and DIJ is the angular diameter distances.
The time delay is observable if the source is variable,
and can be used to infer H0
(Refsdal 1964).
Crucial in this argument is
a proper modelling of the mass distribution of the deflector.
The DD/D factor depends on
 only weakly; its
only weakly; its
 dependence is even weaker.
dependence is even weaker.
 = 0.3)
with a simple galaxy model of a singular isothermal ellipsoid.
For B1608+656,
Koopmans &
Fassnacht (1999)
obtained 64 ± for
= 0.3)
with a simple galaxy model of a singular isothermal ellipsoid.
For B1608+656,
Koopmans &
Fassnacht (1999)
obtained 64 ± for  = 0.3
(59 ± 7 for EdS). For PKS1830-211,
they gave 75+18-10
for EdS and 85+20-11 for
= 0.3
(59 ± 7 for EdS). For PKS1830-211,
they gave 75+18-10
for EdS and 85+20-11 for
 = 0.3
from the time delay measured by
Lovell et
al. (1998).
More work is clearly needed to exhaust the class of models, but
these three lens systems
seem considerably simpler than the first two examples.
Koopmans & Fassnacht concluded 74 ± 8 for low density cosmologies
(69 ± 7 for EdS) from four (excluding the second) lensing
systems using the simplest model of deflectors.
It is encouraging to find
a good agreement with the values from the ladder argument, though the current
results from lenses are still less accurate than the ladder value.
It would be important to ask whether H0 < 60 or
> 80 is possible within
a reasonable class of deflector models.
= 0.3
from the time delay measured by
Lovell et
al. (1998).
More work is clearly needed to exhaust the class of models, but
these three lens systems
seem considerably simpler than the first two examples.
Koopmans & Fassnacht concluded 74 ± 8 for low density cosmologies
(69 ± 7 for EdS) from four (excluding the second) lensing
systems using the simplest model of deflectors.
It is encouraging to find
a good agreement with the values from the ladder argument, though the current
results from lenses are still less accurate than the ladder value.
It would be important to ask whether H0 < 60 or
> 80 is possible within
a reasonable class of deflector models.