


3.1.5. Peculiar velocity - density relation
This is one of the most traditional methods to estimate the cosmic mass density. The principles are spelled out by Peebles (1980). There are two basic tools depending on the scale. For small scales (r < 1 Mpc) the perturbations developed into a non-linear regime, and the statistical equilibrium argument is invoked for ensemble averages that the peculiar acceleration induced by a pair of galaxies is balanced by relative motions (cosmic virial theorem). For a large scale (r > 10 Mpc), where perturbations are still in a linear regime, the basic equation is
with
Small-scale velocity fields:
The status is summarised in
Peebles (1999),
where he has concluded
Beyond a 10 Mpc scale, linear perturbation theory applies. An integral form
of (12) for a spherical symmetric case
(v / H0 r =
Peebles (1995)
argued that the configuration and kinematics of
galaxies are grown following the least action principle
from the nearly homogeneous primeval mass distribution.
Applying this formalism to Local Group galaxies,
he inferred
Large scale velocity fields:
There are a few methods to analyse the large-scale velocity fields
based on (12). The direct use of (12) is a comparison of the density
field derived from redshift surveys with measured peculiar velocities.
Alternatively, one may use the density field reconstructed from
observed velocity field for comparison with the actual density field,
as in the POTENT programme
(Dekel et al. 1990).
A variant of the first method is to observe the anisotropy in redshift space
(redshift distortion)
(Kaiser 1987).
As linear theory applies,
The difficulty is that one needs
accurate information for velocity fields, for which an accurate estimate
of the distances is crucial. Random errors of the distance indicators
introduce large noise in the velocity field. This seems particularly serious
in the POTENT algorithm, in which the
derivative 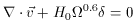
 the density contrast. The
contribution from a cosmological constant is negligible.
The problem inherent in all arguments involving velocity is
the uncertainty regarding the extent to which
galaxies trace the mass distribution (biasing),
or how much mass is present far away from galaxies.
the density contrast. The
contribution from a cosmological constant is negligible.
The problem inherent in all arguments involving velocity is
the uncertainty regarding the extent to which
galaxies trace the mass distribution (biasing),
or how much mass is present far away from galaxies.
 (10 kpc
(10 kpc
 r
r
 1 Mpc) = 0.15 ± 0.10 from
the pair wise velocity dispersion (with samples excluding clusters)
and the three point correlation function of
galaxies via a statistical stability argument.
Bartlett &
Blanchard (1996)
argued that it is possible to reconcile the observed velocity dispersion
with
1 Mpc) = 0.15 ± 0.10 from
the pair wise velocity dispersion (with samples excluding clusters)
and the three point correlation function of
galaxies via a statistical stability argument.
Bartlett &
Blanchard (1996)
argued that it is possible to reconcile the observed velocity dispersion
with  ~ 1
if one assumes galactic halo extended beyond > 300 kpc. As
Peebles (1999)
argued, however, the halo is unlikely to be extended that much
as indicated by the agreement of MW's mass at 100-200kpc and the
mass estimate for MW + M31 in the Local Group.
~ 1
if one assumes galactic halo extended beyond > 300 kpc. As
Peebles (1999)
argued, however, the halo is unlikely to be extended that much
as indicated by the agreement of MW's mass at 100-200kpc and the
mass estimate for MW + M31 in the Local Group.
 0.6
<
0.6
<  >/3) applied to the Virgocentric
flow gives
>/3) applied to the Virgocentric
flow gives 
 0.2 for v
0.2 for v
 200-400 km s-1 and
<
200-400 km s-1 and
<  > ~ 2, assuming no biasing
(Davis and Peebles
1983).
Recently,
Tonry et al. (1999)
argued that
the peculiar velocity ascribed to Virgo cluster is only 140 km s-1,
while the rest of the peculiar velocity flow is attributed to the
Hyd-Cen supercluster and the quadrupole field.
For this case
> ~ 2, assuming no biasing
(Davis and Peebles
1983).
Recently,
Tonry et al. (1999)
argued that
the peculiar velocity ascribed to Virgo cluster is only 140 km s-1,
while the rest of the peculiar velocity flow is attributed to the
Hyd-Cen supercluster and the quadrupole field.
For this case 
 0.06. We may have
0.06. We may have
 ~ 1
only when half the mass is well outside the galaxies.
~ 1
only when half the mass is well outside the galaxies.
 = 0.15 ±
0.15. On the other hand,
Branchini &
Carlberg (1994) and
Dunn & Laflamme
(1995)
argued that this conclusion is not tenable
if mass is distributed smoothly outside galaxies as in
= 0.15 ±
0.15. On the other hand,
Branchini &
Carlberg (1994) and
Dunn & Laflamme
(1995)
argued that this conclusion is not tenable
if mass is distributed smoothly outside galaxies as in
 = 1 CDM models.
This seems, however, not very likely
unless mass distribution is extended over 10 Mpc scale
(Peebles 1999).
= 1 CDM models.
This seems, however, not very likely
unless mass distribution is extended over 10 Mpc scale
(Peebles 1999).
 always appears in the combination
always appears in the combination
 =
=
 0.6 / b where
b
is a linear biasing factor of galaxies against the mass distribution
and can be inferred through non-linear effects.
Much effort has been invested in such analyses (see e.g.,
Strauss & Willick
1995;
Dekel et al. 1997;
Hamilton 1998),
but the results are still controversial.
The value of
0.6 / b where
b
is a linear biasing factor of galaxies against the mass distribution
and can be inferred through non-linear effects.
Much effort has been invested in such analyses (see e.g.,
Strauss & Willick
1995;
Dekel et al. 1997;
Hamilton 1998),
but the results are still controversial.
The value of  0.6 / b
derived from many analyses varies from
0.3 to 1.1, though we see a general trend to favour a high value.
Notably, the most recent POTENT analysis using
the Mark III compilation of velocities
(Willick et
al. 1997)
indicates
a high density universe
0.6 / b
derived from many analyses varies from
0.3 to 1.1, though we see a general trend to favour a high value.
Notably, the most recent POTENT analysis using
the Mark III compilation of velocities
(Willick et
al. 1997)
indicates
a high density universe  =
0.5-0.7, and
=
0.5-0.7, and  > 0.3 only at
a 99% confidence level
(Dekel et al. 1999).
> 0.3 only at
a 99% confidence level
(Dekel et al. 1999).
 .
.
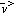 /
/
 0.6
and its square are numerically computed; this
procedure enhances noise, especially for a small
0.6
and its square are numerically computed; this
procedure enhances noise, especially for a small
 .
The difficulty of inferring large scale velocity
field may also be represented by the `great attractor problem'.
Lynden-Bell et
al. (1988)
found a large-scale velocity field towards the
Hyd-Cen supercluster, but also argued that this supercluster is also
moving towards the same direction attracted by a `great (giant) attractor'.
With
Tonry et al.'s
(1999)
new estimate of the distance using SBF,
this velocity field is modest, and Hyd-Cen itself serves as
the great attractor that pulls the Virgo cluster,
with the conclusion that
.
The difficulty of inferring large scale velocity
field may also be represented by the `great attractor problem'.
Lynden-Bell et
al. (1988)
found a large-scale velocity field towards the
Hyd-Cen supercluster, but also argued that this supercluster is also
moving towards the same direction attracted by a `great (giant) attractor'.
With
Tonry et al.'s
(1999)
new estimate of the distance using SBF,
this velocity field is modest, and Hyd-Cen itself serves as
the great attractor that pulls the Virgo cluster,
with the conclusion that  is small.
is small.