Essay

PHASE TRANSITION

Adapted from P. Coles, 1999, The Routledge Critical Dictionary of the New Cosmology, Routledge Inc., New York. Reprinted with the author's permission. To order this book click here: http://www.routledge-ny.com/books.cfm?isbn=0415923549

A change from a disordered high-energy state into an ordered low-energy state, undergone by matter as it cools down. For example, a liquid is quite disordered, while a crystal is highly regular and ordered. In the very early stages of the Big Bang, it is thought that, as matter cooled, it underwent many such changes, during the course of which the Universe's state of symmetry (roughly speaking, the properties of elementary particles and the apparent form of the fundamental interactions) was altered. This happened in such a way that the present-day low-energy, low-temperature Universe does not appear to possess the symmetries that it should have in unified theories of the fundamental interactions, such as grand unified theories.

To visualise how this might happen, imagine standing on the ridge of a roof. On either side of you, the roof slopes away in a completely symmetrical fashion. If you fall, there is nothing about the roof that would make you fall down the left or the right side. But if you do fall, perhaps blown over by a random gust of wind, you can fall only one way. As you descend to your low-energy state, you have broken the symmetry of the situation (and possibly a few limbs). This analogy emphasises the point that the outcomes of given physical laws do not necessarily have the same symmetry as the laws themselves. Likewise, as the Universe was cooling it need not necessarily have respected the symmetry of laws that govern its behaviour. This can happen in particular when phase transitions are involved. (For a detailed description of the circumstances in which such effects can occur, and of the different kinds of phase transition possible, see spontaneous symmetry-breaking.)

The model of spontaneous symmetry-breaking has been widely used to study the behaviour of particle interactions in theories of the fundamental interactions. Because phase transitions of the required type are expected to appear in the early Universe according to standard particle physics models, the initial stages of the Big Bang are often described as the era of phase transitions. One important idea, which we shall refer to later, is that we can identify an order parameter Phi , which is small in the high-temperature disordered state and grows during the phase transition, with the value of a particular quantum scalar field, such as the so-called Higgs field that occurs in some quantum field theories. The free energy related to the scalar field can be related to the effective potential of the field V( Phi ) (which describes its interactions).

In the standard Big Bang theory, the thermal history of the Universe during the period lasting from the Planck time or thereabouts (where the temperature was some 10³² K) until the moment when quarks combined into hadrons, which happened when the temperature was about 10¹² K, is punctuated by a series of phase transitions (not all of which are well understood). Some of these transitions and their consequences are described below. It is convenient to express the temperature in terms of the equivalent energy in electronvolts (eV), the unit favoured by experimental particle physicists. The Planck temperature, 10³² K, corresponds to about 10¹⁹ GeV (where 1 GeV is 10⁹ eV) - far higher than the energies that can be reached in any terrestrial accelerator experiment. The quark-hadron transition took place at around 300 MeV, (where 1 MeV is 10⁶ eV), which is well within the reach of large accelerators such as that at CERN.

Starting at 10¹⁹ GeV, the first major landmark reached by the cooling Universe was the energy scale at which grand unified theories (GUTs) are thought to have begun to break symmetry, at around 10¹⁵ GeV. In the period before this, quantum gravitational effects are thought to have become negligible, and the particles to have been held in thermal equilibrium by means of interactions described by a GUT. At the GUT temperature, which was reached about 10^-37 seconds after the initial bang, the GUT symmetry began to break. If we assume for the sake of argument that the gauge group describing the GUT physics is the simplest possible, SU(5) (see gauge theory), then at 10¹⁵ GeV the relevant symmetry group would have changed for a period into a different one, SU(3) 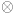circle_cross SU(2) 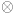U(1) for example, or perhaps some other symmetry. The GUT transition is expected to have resulted in the formation of magnetic monopoles, and perhaps to have given rise to other topological defects.

A GUT, which unifies the electroweak interactions with the strong interactions, puts leptons and hadrons on the same footing and thus allows processes which do not conserve baryon number B (violation of baryon number conservation is not allowed in either quantum chromodynamics or electroweak theory). It is thought, therefore, that processes could occur at the GUT temperature which might create the baryon-antibaryon asymmetry that is observed now (see baryogenesis). Baryons themselves did not form until much later, when the quark-hadron transition had taken place, but at energies where the GUT symmetry is not broken, quarks and antiquarks are equivalent, so a baryon-antibaryon asymmetry cannot have resulted from this phase. The conditions necessary for the eventual creation of a baryon-antibaryon asymmetry were stated in 1967 by Andrei Sakharov. It seems that these conditions prevailed at the GUT scale or slightly lower, depending on the particular version of GUT or other theory adopted; baryogenesis can even occur at much lower energies, around the electroweak scale. Even though this problem is complicated and therefore rather controversial, with reasonable hypotheses we can arrive at a baryon-antibaryon asymmetry of the same order as that observed: about one in a thousand billion (see also antimatter). It is worth noting also that, if the Universe is initially lepton-symmetric, the reactions that violate conservation of baryon number can also produce an excess of leptons over antileptons which is equal, in the case of SU(5) GUTs, to that of the baryons over the antibaryons. This is simply because the GUTs unify quarks and leptons. In a GUT the value of the baryon asymmetry actually produced depends only on fundamental parameters of the theory. This means that, even if the Universe is inhomogeneous, the value of the asymmetry should be the same in any region.

When the temperature fell below 10¹⁵ GeV, the strong and electroweak interactions decoupled. The super-heavy bosons that mediate the GUT interaction now rapidly disappeared through annihilation or decay processes. In the moment of symmetry-breaking the order parameter Phi , whose appearance signalled the phase transition proper, could assume a different `sign' or `direction' in adjoining spatial regions. It is thus possible that Phi could have changed rapidly with spatial position, between one region and another. (This is similar to the `Bloch walls' which, in a ferromagnet, separate the different magnetised domains of magnetisation.) The `singular' regions in which Phi was discontinuous would have had a structure that depended critically on the symmetry that had been broken, giving rise to different possible types of topological defect.

Although the strong interaction separated from electroweak interactions at about 10^-37 seconds, the electroweak theory kept its form until much later, about 10^-11 seconds after the beginning. It is probable that phase transitions occurred in this period which are not yet well understood. The particles we are considering here range in energy from 10² to 10¹⁵ GeV; within the framework of the SU(5) model discussed above there are no particles predicted to have masses in this range of energies, which is consequently known as the grand desert. Nevertheless, there remain many unresolved questions about this epoch. In any case, of the end of this period we can safely say that, to a good approximation, the Universe would have become filled with an ideal gas containing leptons and anti-leptons, the four vector bosons, quarks and antiquarks and gluons (see elementary particles). At a temperature of a few hundred GeV there would have been a spontaneous breaking of the SU(2) 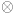circle_cross U(1) symmetry that describes the electroweak theory, through a phase transition which was probably of first order. All the leptons acquired masses (with the probable exception of the neutrinos), while the intermediate vector bosons gave rise to the massive bosons now known as the W and Z particles, and to photons. The massive bosons disappeared rapidly by decay and annihilation processes when the temperature fell below about 90 GeV.

The last phase transition in this sequence occurred when the temperature had fallen still further, to around 300 MeV. In the framework of QCD theory, the strong interactions then became very strong indeed and led to the confinement of quarks into hadrons, signalling the start of the quark-hadron phase transition, after which came the (very short-lived) hadron era. The remaining events from that time onward are described in the entry on the thermal history of the Universe.