
Adapted from P. Coles, 1999, The Routledge Critical Dictionary of the New Cosmology, Routledge Inc., New York. Reprinted with the author's permission. To order this book click here: http://www.routledge-ny.com/books.cfm?isbn=0415923549
While the Universe may be roughly homogeneous and isotropic on the scale of our horizon, as required by the cosmological principle, the distribution of galaxies in space is decidedly inhomogeneous on scales smaller than this (see large-scale structure). In order to quantify the lumpiness of the matter distribution revealed by redshift surveys and to relate this to models of structure formation, cosmologists employ a variety of statistical tools, the most common of which is called the power spectrum and which is usually given the symbol P(k).
The power spectrum is defined in the mathematical language of
Fourier series. The simplest way to define it is to define a
fluctuation field  (x) at different spatial locations x in terms of
the actual density of matter
(x) at different spatial locations x in terms of
the actual density of matter  (x) at the position x, and
subtract the
mean density of matter
(x) at the position x, and
subtract the
mean density of matter  0:
0:
Because this departure from the mean density is divided by the mean
density, the resulting
Suppose we consider a part of the Universe contained within a cubic
volume V of side L (V =
L3). Assuming (for mathematical purposes only)
that the Universe outside this cube consists of periodic replications
of what is inside, we can expand
The sum is taken over all the waves that fit into the periodic box.
These waves have wave-vectors k of the form
(kx, ky, kz) =
(nx, ny,
nz)2
Fourier coefficients
where the summation is now over all modes, and the average is over all
possible boxes with the same volume V. We can interpret
where P(k) is the power spectrum or, more precisely, the power
spectral density function. Despite its rather involved derivation,
P(k) is quite simple to visualise: it represents the contribution to
the fluctuation field from waves of wavenumber k (and therefore
wavelengths
In most theories of cosmological structure formation there are
initial primordial density fluctuations specified by a very simple
power-law form: P(k)
Knowing T(k) then allows us to define the initial conditions for a
detailed computation of the evolution of density fluctuations.
The advantages of the power spectrum as a way of characterising
density fields are many. Firstly, in the gravitational Jeans
instability, as long as the fluctuations are small (
On smaller scales where nonlinear (non-perturbative) effects are
important, the power spectrum changes shape but it does not lose its
usefulness. We can compute the power spectrum in an N-body
simulation
of a model, for example, and use it to test the model in question
against observations, from which the power spectrum can be estimated
quite easily.
Another advantage for the initial stages of clustering evolution is
linked to the statistical properties of the initial fluctuations. In
most theories, including the inflationary Universe models, the initial
seed irregularities are Gaussian. This means that the power spectrum
alone furnishes a complete statistical description of the
fluctuations. Know the power spectrum, and you know it all.
There is also an important connection between P(k) and the method
that has been historically important for quantifying the distribution
of galaxies in space: the two-point correlation function,
FURTHER READING:
Harrison, E.R., `Fluctuations at the threshold of classical
cosmology', Physical Review D, 1970, 1, 2726.
Zel'dovich, Ya.B., `A hypothesis unifying the structure and entropy of
the Universe', Monthly Notices of the Royal Astronomical Society,
1972, 160, 1P.
Coles, P., `The large-scale structure of the Universe', Contemporary
Physics, 1996, 37, 429.
Coles, R and Lucchin, F., Cosmology: The Origin and Evolution of
Cosmic Structure (John Wiley, Chichester, 1995), Chapter 14.
 (x) = (
(x) = ( (x) -
(x) -  0) /
0) /  0
0
 is
dimensionless; it is usually called the density contrast.
is
dimensionless; it is usually called the density contrast.
 in a Fourier series representing a
superposition of plane waves with different amplitudes:
in a Fourier series representing a
superposition of plane waves with different amplitudes:
 (x) =
(x) = 
 (k) exp(ik . x)
(k) exp(ik . x)
 / L,
where the nx etc. are integers. The
/ L,
where the nx etc. are integers. The
 (k) for each mode are complex numbers having
both an amplitude and a phase. If instead of the volume V we had
chosen a different volume V', we would have found that the same series
expansion would be possible but that the co-efficients were a
different set of complex numbers. We can imagine repeating this
box-shifting idea for a huge number of boxes all around the
Universe. It would then be possible to calculate statistical averages
over these Fourier coefficients, such as the average squared modulus
of
(k) for each mode are complex numbers having
both an amplitude and a phase. If instead of the volume V we had
chosen a different volume V', we would have found that the same series
expansion would be possible but that the co-efficients were a
different set of complex numbers. We can imagine repeating this
box-shifting idea for a huge number of boxes all around the
Universe. It would then be possible to calculate statistical averages
over these Fourier coefficients, such as the average squared modulus
of  (k), which we
can write as <
(k), which we
can write as <  (k)
(k)  *
(k) >, where the * denotes a
complex conjugate. We can then define the quantity
*
(k) >, where the * denotes a
complex conjugate. We can then define the quantity  k as
k as
 <
<  (k)
(k)  * (k) > = (1 / V)
* (k) > = (1 / V) 
 k2
k2
 k as being a
kind of average amplitude for waves with wave-vector k. If the
distribution of matter is statistically homogeneous and isotropic,
then this average will not depend on the direction of k, just its
magnitude k. The final step in this definition is now to let the
volume V tend to infinity; the right-hand side of the above equation
is then
k as being a
kind of average amplitude for waves with wave-vector k. If the
distribution of matter is statistically homogeneous and isotropic,
then this average will not depend on the direction of k, just its
magnitude k. The final step in this definition is now to let the
volume V tend to infinity; the right-hand side of the above equation
is then

 k2 = (1 /
2
k2 = (1 /
2 2)
2) 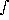 P(k)k2 dk
P(k)k2 dk
 = 2
= 2 /k). A completely flat power
spectrum corresponds
to white noise (i.e. equal power at all frequencies), while a power
spectrum that is sharply peaked at some particular value of k has a
characteristic length scale. A single plane wave has a power spectrum
consisting of a single spike.
/k). A completely flat power
spectrum corresponds
to white noise (i.e. equal power at all frequencies), while a power
spectrum that is sharply peaked at some particular value of k has a
characteristic length scale. A single plane wave has a power spectrum
consisting of a single spike.
 kn. In most versions of the inflationary
Universe the power spectrum has an index n very close to 1, which is
called the scale-invariant or Harrison-Zel'dovich spectrum. The
situation is a little more complicated than this in realistic models
of structure formation, because this initial spectral shape can be
modified by non-gravitational processes in the period before
recombination: Silk damping, free streaming and the
Meszaros effect
can all alter the shape of P(k). Given any particular detailed model,
however, these effects can be modelled and they are usually
represented in terms of a transfer function T(k) for the model such
that
kn. In most versions of the inflationary
Universe the power spectrum has an index n very close to 1, which is
called the scale-invariant or Harrison-Zel'dovich spectrum. The
situation is a little more complicated than this in realistic models
of structure formation, because this initial spectral shape can be
modified by non-gravitational processes in the period before
recombination: Silk damping, free streaming and the
Meszaros effect
can all alter the shape of P(k). Given any particular detailed model,
however, these effects can be modelled and they are usually
represented in terms of a transfer function T(k) for the model such
that
 much less than
1) we can solve the equations describing their evolution using
perturbation theory. We find that the shape of the power spectrum is
not changed by gravitational evolution: only the amplitude increases
as a function of time. To put this another way, in perturbation theory
all the Fourier modes evolve independently, so that the amplitude of
each mode increases at the same rate. Assuming that the power spectrum
decreases with decreasing k (increasing wavelength), which it must do
if the Universe is to be smooth on large scales, this means that the
power spectrum for small k should retain its primordial shape. This
allows astronomers to probe the primordial density fluctuations
directly by using observations of galaxy clustering.
much less than
1) we can solve the equations describing their evolution using
perturbation theory. We find that the shape of the power spectrum is
not changed by gravitational evolution: only the amplitude increases
as a function of time. To put this another way, in perturbation theory
all the Fourier modes evolve independently, so that the amplitude of
each mode increases at the same rate. Assuming that the power spectrum
decreases with decreasing k (increasing wavelength), which it must do
if the Universe is to be smooth on large scales, this means that the
power spectrum for small k should retain its primordial shape. This
allows astronomers to probe the primordial density fluctuations
directly by using observations of galaxy clustering.
 (r). Together
these two functions form a Fourier transform pair, so
they provide completely equivalent information about the fluctuation
field. A very similar concept to P(k) can be used to describe the
fluctuations in temperature on the (two-dimensional) celestial sphere,
rather than in three-dimensional space.
(r). Together
these two functions form a Fourier transform pair, so
they provide completely equivalent information about the fluctuation
field. A very similar concept to P(k) can be used to describe the
fluctuations in temperature on the (two-dimensional) celestial sphere,
rather than in three-dimensional space.